Найдите все значения параметра а при каждом из которых система уравнений имеет ровно три решения
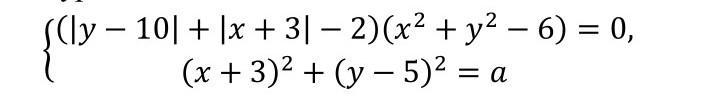
Ответы
Ответ: 3 решения будет , когда a∈{49} ∪ {4*(10-√51)}
Объяснение:
Рассмотрим уравнение 1 :
(|y-10|+|x+3|-2)*(x^2+y^2-6)=0
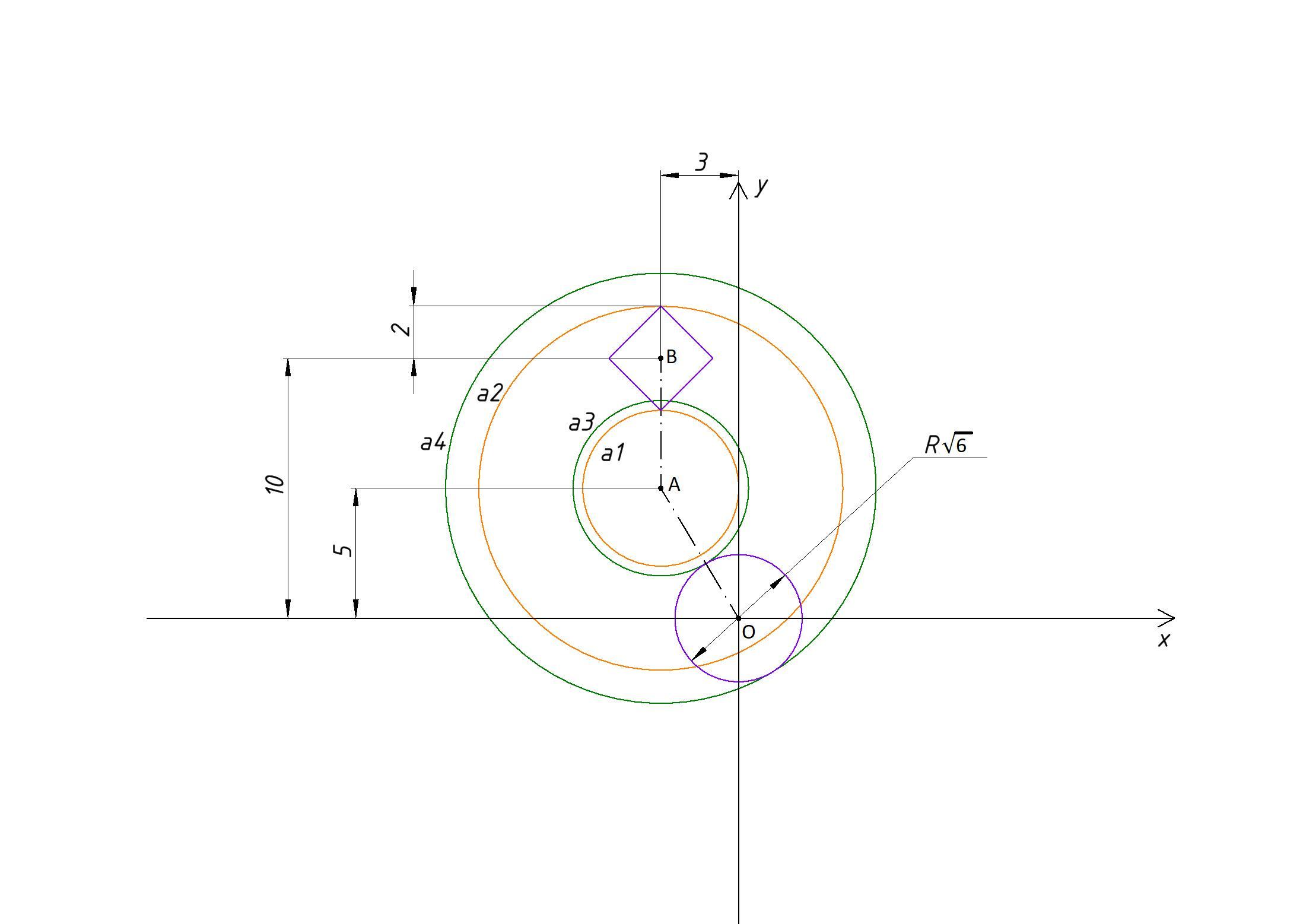
Уравнение представляет собой совокупность квадрата с центром в точке: B(-3;10) с половиной диагонали равной 2 и окружность с центром в начале координат и радиусом √6.
Рассмотрим уравнение 2
(x+3)^2+(y-5)^2=a -окружность с центром в точке : A (-3 ;5) и радиусом равным √a (находится на одной вертикали с квадратом из уравнения 1)
На рисунке показаны случаи касания окружности из уравнения к окружности и к квадрату из уравнения 1.
3 решения будет либо когда окружность из уравнения 2 касается квадрата (в 1 точке ) и пересекает окружность уравнения 1 ( в двух точках соответственно) , либо когда касается окружности уравнения и пересекает квадрат ( в двух точках соответственно).
Все обозначения смотрите на рисунке.
Найдем расстояния между центрами:
AB=10-5=5
AO=√(5^2+3^2)=√34
a1=5-2=3 → a=3^2=9
a2=5+2=7 → a=7^2=49
a3=√34-√6=√2* (√17-√3) → a= (√2* (√17-√3) )^2=40-4√51=4*(10-√51)
a4=√34+√6=√2*(√17+√3) → a= (√2*(√17+√3) )^2=4*(10+√51)
Cравним: a1 и a3
3 и √2* (√17-√3)
9 и 40-4*√51
4√51 и 31
816 < 961
Так же очевидно ,что :
a4=√34+√6 >√25+√4 =7=a2
a3=√34-√6<√49=7=a2
a4>a2>a3>a1
Тогда из рисунка видно, что 3 решения получается когда :
a=a3^2=4*(10-√51)
a= a2^2=49
a∈{49} ∪ {4*(10-√51)}
Теперь рассмотрим отдельно то , когда a=0
В этом случае уравнение 2 имеет вид :
(x+3)^2 +(y-5)^2=0
Поскольку квадрат число неотрицательное , то
x=-3 ; y=5
Но эта точка не принадлежит области первого уравнения.
Ответ : 3 решения будет , когда a∈{49} ∪ {4*(10-√51)}