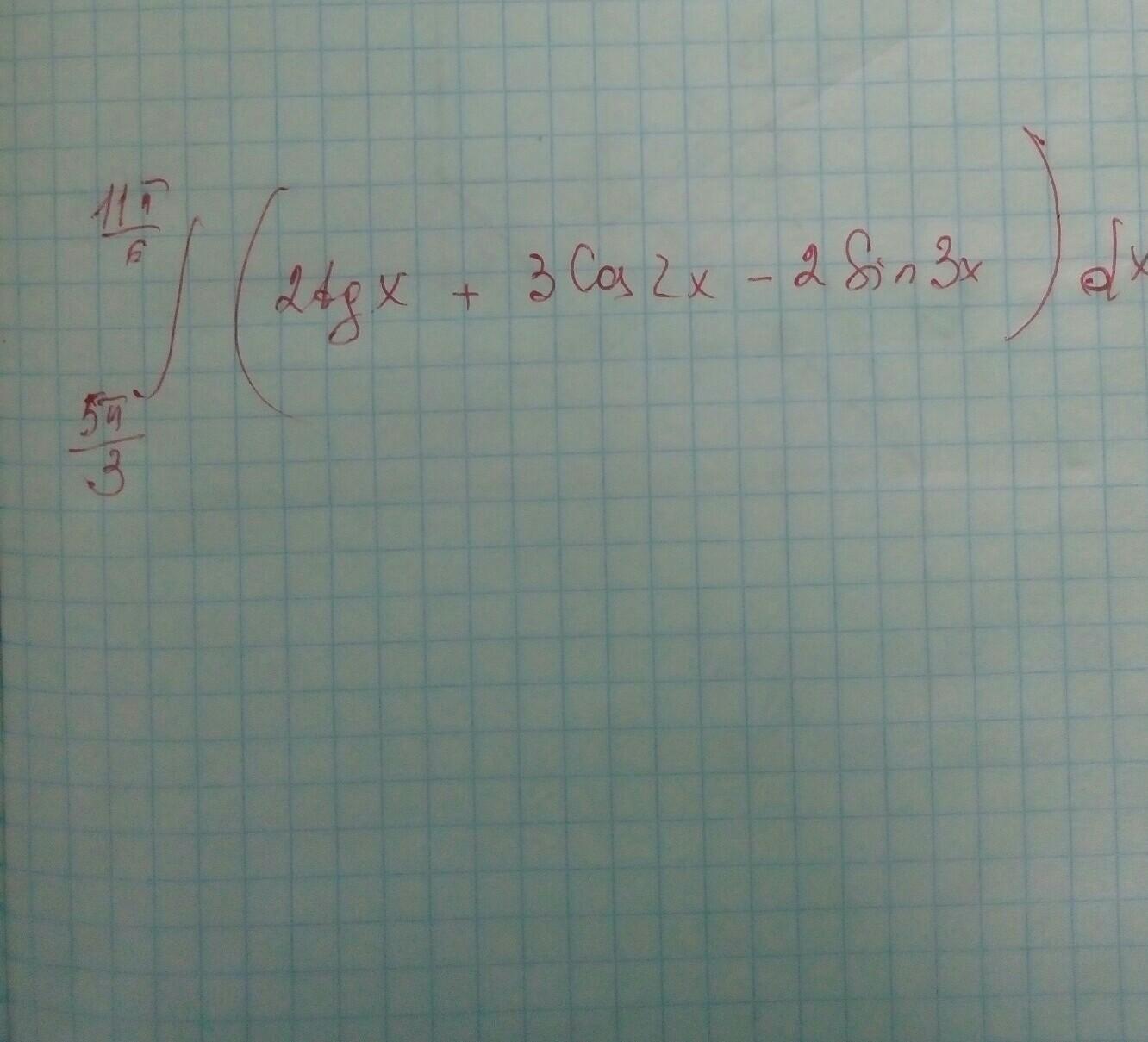Question

помогите пожалуйста,срочно,35 баллов даю​

Answer 1

Ответ:

Пошаговое объяснение:

∫(границы поставишь)(2tgx+3cos2x-2sin3x)dx=2∫tgxdx+3∫cosx2xdx--2∫sin3xdx=2∫sinx/cosxdx+3/2∫cosxd(2x)-2/3∫sin3xd(3x)=-2∫d(cosx)/cosx+

+3/2sin2x(вертикальная черта границы)+2/3cos3x(границы)=-2ln|cosx|(границы)+3/2(sin(11Pi/3)-sin(10pi/3))+2/3(cos(11pi/2)-

-cos(5pi))=-2ln(cos(11pi/6)-

-cos(5pi/3))+3/2*sin(pi/3)+2/3cos(pi/2)=-2ln|cos(pi/6)|+3/2*√3/2+2/3*0=

=-2ln√3/2+3√3/4