Question

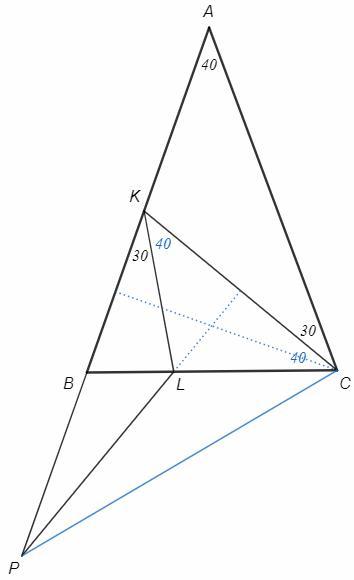
В равнобедренном треугольнике ABC (АВ = АС) угол при вершине A равен 40. На сторонах
AB и BC выбраны точки K и L соответственно так, что ACK= BKL = 30. На продолжении
стороны AB за точку B выбрана точка P так, что AK = BP. Найдите угол APL

Answer 1

Углы при основании BAC равны 70, угол BCK=40, треугольник BCK - равнобедренный, угол CKL=40, треугольник CLK - равнобедренный. Точка L лежит на серединном перпендикуляре к CK.

Точка C лежит на серединном перпендикуляре к BK, следовательно и на серединном перпендикуляре к PA, AC=PC, APC=A=40.

PK=AB=AC=PC, точка P лежит на серединном перпендикуляре к BK. Следовательно PL - серединный перпендикуляр к BK и биссектриса KPC, APL=40/2=20.