Решите неравенство √(x-4)>10-x

Ответы

Ответ дал: dnepr1

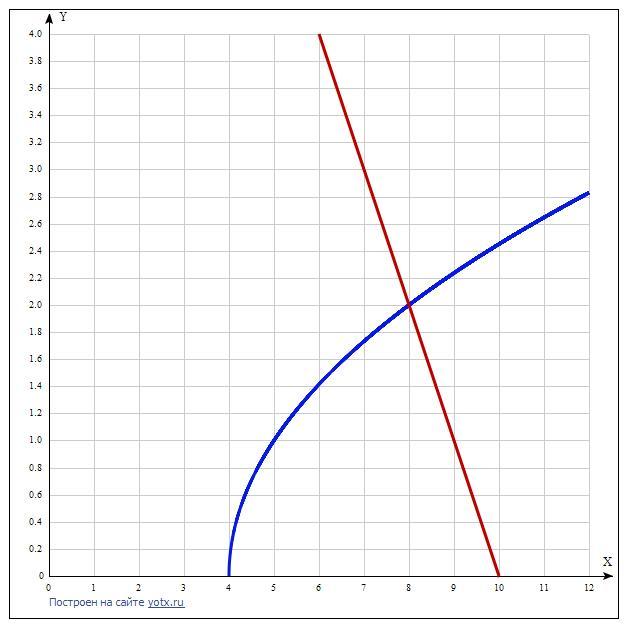
Дано неравенство √(x-4)>10-x. ОДЗ: х ≥ 4.

Левая часть - возрастающая функция, правая - убывающая.

Значит, есть одна точка пересечения, после которой справедливо неравенство.

Возведём его в квадрат: x-4>100 - 20x + x².

Приведём подобные: x² - 21x + 104 < 0.

Находим нули: x² - 21x + 104 = 0. Д = 441 - 4*104 = 25.

х1 = (21 + 5)/2 = 13, х2 = (21 - 5)/2 = 8.

С учётом ОДЗ принимаем значение х = 8.

Ответ: х > 8.

Приложения:

s0807: А почему мы выбираем значение 8? А не 13

antonovm: 1)"Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, после которой справедливо неравенство." -это неверно , так как может случится так , что общих точек нет

antonovm: 2) для нахождения общих точек надо приравнять f(x) и g(x) , а не возводить обе части неравенства в квадрат

antonovm: 3) возводить в квадрат можно , если обе части неравенства положительны , а здесь при х > 10 правая часть отрицательна ,

antonovm: 4) и действительно , если учитывать ОДЗ , то непонятно почему 13 не подходит

antonovm: как раз ОДЗ тут не при чем , 13 не подходит , но по другой причине

dnepr1: Вот почему 13 не подходит: надо в ОДЗ добавить 10 - х > 0, x < 10.

Вас заинтересует

Математика

1 год назад

Помогитееее!!!!!20баллов дам

Биология

1 год назад

значення рослин для планети допоможіть написати