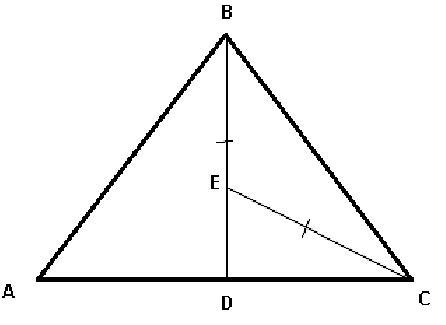
На медіані ріанобедреного трикутника,проведеній до основи,взято точку,що однаково віддалена від кінців бічної сторони.Обчисліть периметр трикутника,якщо відстань від цієї точки до основи дорівнює 14 см, а до кінця основи - 50 см.
Аноним:
256
Ответы
Ответ дал:
1
Пусть точка Е лежит на медиане BD равнобедренного треугольника
ED = 14 см и CE = 50 см. Поскольку отрезки от концов боковой
стороны равноудалены, то BE = CE = 50 см. Из прямоугольного
треугольника EDC по теореме Пифагора:
см
Поскольку BD - медиана равнобедренного треугольника, то
она является и высотой и биссектрисой. Тогда BD = 14+50 = 64 см.
По теореме Пифагора из прямоугольного треугольника BDC:
см.
AC = 2 * DC = 2 * 48 = 96 см. Тогда периметр треугольника равен
P = AB + BC + AC = 80 + 80 + 96 = 256 см
Приложения:
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад