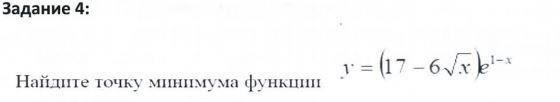Ответы
Ответ дал:
0
y`=(17-6√x)`·e¹⁻ˣ+(17-6√x)·(e¹⁻ˣ)`=
x=9 - точка минимума, так как производная меняет знак с - на +
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад