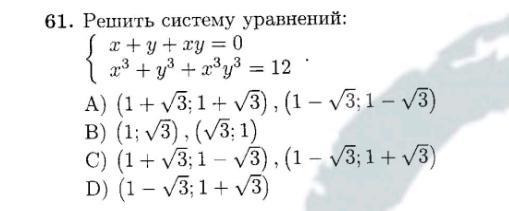Ответы
Ответ дал:
1
Ответ:
Приложения:

Ответ дал:
2
Ответ:
C
Объяснение:
Приложения:

antonovm:
при переходе к z использована теорема , обратная к теореме Виета , так как x и y симметричны , то в решении будут 2 пары , у второй меняются местами переменные
Вообще это симметрическая система ( уравнения не меняются , если заменить х на y и наоборот и они решаются именно с помощью этой замены
системы можно решать и без Виета ( подстановкой) , будет не очень красиво , но ответ тот же
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад