Помогите решить уравнения
Приложения:
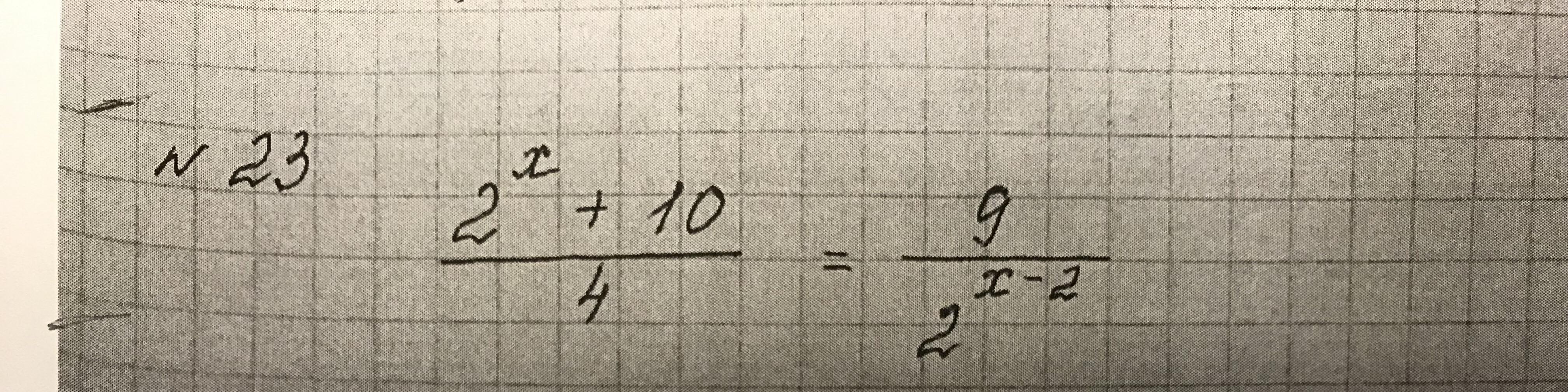
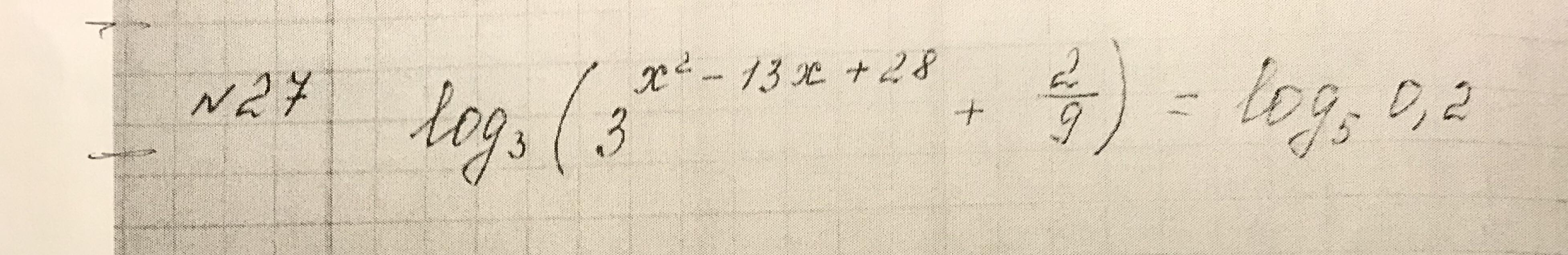
Аноним:
№25; х=3. Если зададите, напишу решение.
№23. Первое. Описка...
Ответы
Ответ дал:
1
23)
27)
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
8 лет назад