Дана правильная треугольная призма ABCA1B1C1 с основаниями ABC и A1B1C1. Скрещивающиеся диагонали BA1 и CB1 боковых граней AA1B1B и BB1C1C перпендикулярны.
Докажите, что AB:AA1=√2:1.
Ответы
Ответ дал:
1
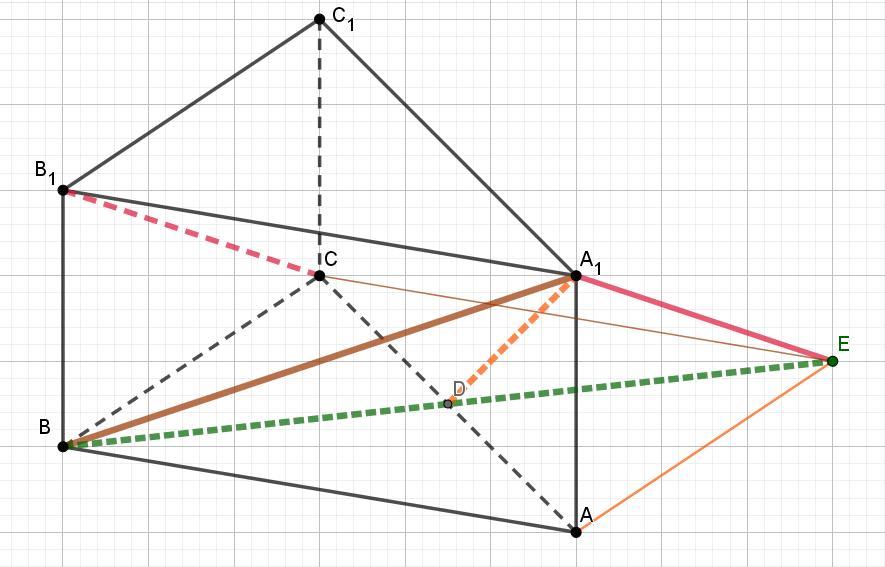
Перенесём диагональ СВ1 точкой В1 в точку А1.
Получим прямоугольный равнобедренный треугольник ВА1Е.
Примем длину основания призмы за "а", высоту за "h".
Сторона ВЕ равна двум высотам АВС:
ВЕ = 2а*(√3/2) = а√3.
Рассмотрим высоту А1Д треугольника ВА1Е.
А1Д = (1/2)ВЕ = а√3/2.
С другой стороны, А1Д - это гипотенуза треугольника АА1Д.
По Пифагору (А1Д)² = (а/2)² + h².
h = √((3a²/4) - (a²/4) = √(2a²/4) = a/√2.
Найдём соотношение AB:AA1 = а/(a/√2) = √2/1.
Ответ: AB:AA1=√2:1.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад