Question

Помоги пожалуйста задание во вложении​

Answer 1

Ответ:

Объяснение:

Ответ:

25

Объяснение:

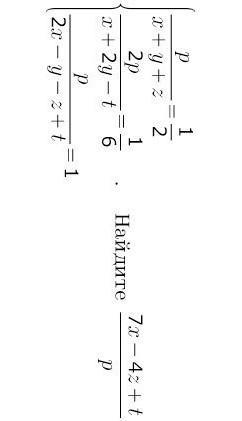
p/(x+y+z)=1/2

2p/(x+2y-t)=1/6

p/(2x-y-z+t)=1

2p=x+y+z

12p=x+2y-t

p=2x-y-z+t

12p-2p=x+2y-t-x-y-z

10p=y-t-z

10p+p=y-t-z+2x-y-z+t

11p=2x-2z

2(x-z)=11p

x-z=5,5p

x=5,5p+z

2p=5,5p+z+y+z

2p-5,5p=2z+y

-3,5p=2z+y

y=-3,5p-2z

p=2(5,5p+z)-(-3,5p-2z)-z+t=11p+2z+3,5p+2z-z+t=14,5p+3z+t

p-14,5p=3z+t

3z+t=-13,5p

t=-13,5p-3z

(7x-4z+t)/p=(7(5,5p+z)-4z-13,5p-3z)/p=(38,5p+7z-4z-13,5p-3z)/p=25p/p=25

Answer 2

Перевернем дробь в трех уравнениях, получим систему вида

$\begin{cases}&\text{}\dfrac{x+y+z}{p}=2\\&\text{}\dfrac{x+2y-t}{p}=12\\&\text{}\dfrac{2x-y-z+t}{p}=1\end{cases}$

Данное решение приводится к методу неопределённых коэффициентов

$\dfrac{7x-4z+t}{p}=A\left(\dfrac{x+y+z}{p}\right)+B\left(\dfrac{x+2y-t}{p}\right)+C\left(\dfrac{2x-y-z+t}{p}\right)\\ \\ 7x-4z+t=(A+B+2C)x+(A+2B-C)y+(A-C)z+(C-B)t$

Приравниваем коэффициенты при x,y,z,t, получим

$\begin{cases}&\text{}A+B+2C=7\\&\text{}A+2B-C=0\\&\text{}A-C=-4\\&\text{}C-B=1\end{cases}~\Rightarrow~\begin{cases}&\text{}B-3C=-7\\&\text{}-B+C=1\\&\text{}A-C=-4\\&\text{}A+2B-C=0\end{cases}~\Rightarrow~\begin{cases}&\text{}C=3\\&\text{}B=2\\&\text{}A=-1\\&\text{}-1+4-3=0\end{cases}$

Таким образом, $\dfrac{7x-4z+t}{p}=(-1)\cdot 2+2\cdot 12+3\cdot 1=25$

Ответ: 25.