Решите, пожалуйста, наиболее лёгким путём
Приложения:
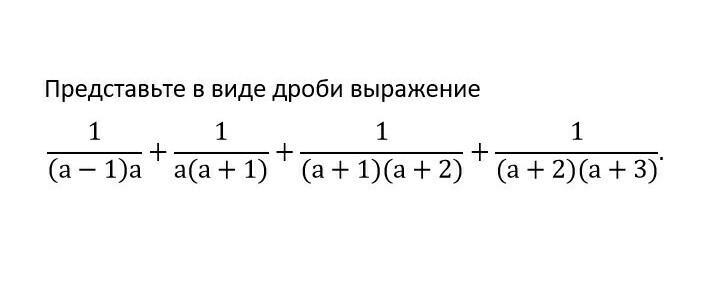
Аноним:
единицу представить как a-a+1
на две дроби разбить
Ответы
Ответ дал:
1
Ответ:
Решение:
Ответ дал:
1
2 способа. Первый подробный. Второй, если сразу использовать готовую формулу.
Приложения:


Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад