ОЧЕНЬ СРОЧНО ,ЗАРАНЕЕ СПАСИБО
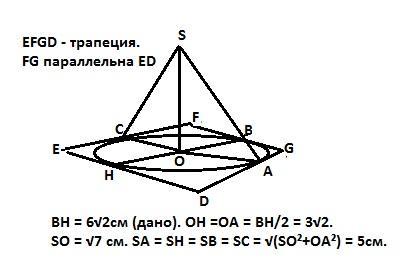
Точка S равноудалена от сторон трапеции и находится на расстоянии √7 см от ее плоскости . Найдите расстояние от точки S до сторон трапеции если её высота равна 6√2 см
Ответы
Ответ:
Расстояние от точки S до сторон трапеции равно 5 см.
Объяснение:
Расстояние от точки S до сторон трапеции - это перпендикуляры, проведенные из этой точки к сторонам. Опустим перпендикуляр SO на плоскость трапеции и соединим точку О с концами перпендикуляров от точки S до сторон. По теореме о трех перпендикулярах проекции расстояния от точки S до сторон перпендикулярны сторонам трапеции. Если наклонные (расстояния от S до сторон) равны, то равны и их проекции. Следовательно, точка S проецируется в центр вписанной в трапецию окружности, радиус которой равен половине высоты трапеции, то есть
R = 3√2 см.
Расстояние от точки S до сторон трапеции - это гипотенуза прямоугольного треугольника с катетами - √7 см и 3√2 см.
По Пифагору: L = √(7+18) = 5 cм.