Question

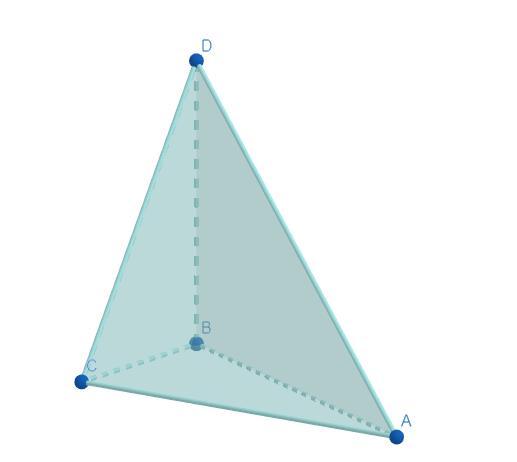
Дана пирамида DABC, в которой DB⊥BC, AB=8, AC=BD=6, AD=10, ∠ACB=90°.
а) Докажите, что DB⊥(ABC); б) Найдите косинус угла между плоскостями (ADC) и (ABC).

Answer 1

a). Заметим, что треугольник ABD египетский. Действительно, BD:AB:AD = 6:8:10 = 3:4:5. Значит, DB ⊥ AB.

DB ⊥ BC, DB ⊥ AB ⇒ DB ⊥ (ABC).

Q.E.D.

б). DB ⊥ (ABC) ⇒ BC  - проекция DC на (ABC).

BC ⊥ AC ⇒ DC ⊥ AC по теореме о трех перпендикулярах.

BC ⊥ AC,  DC ⊥ AC ⇒ ∠((ADC), (ABC)) = ∠DCB.

По теореме Пифагора для ΔACB:

BC² + AC² = AB² ⇒ BC² = 8² - 6² = 28 ⇔ BC = 2√7.

По теореме Пифагора для ΔCBD:

BC² + BD² = CD² ⇒ CD² = 6² + 4·7 = 64 ⇔ CD = 8.

cos∠DCB = BC/CD = 2√7/8 = √7/4.

Ответ: √7/4.