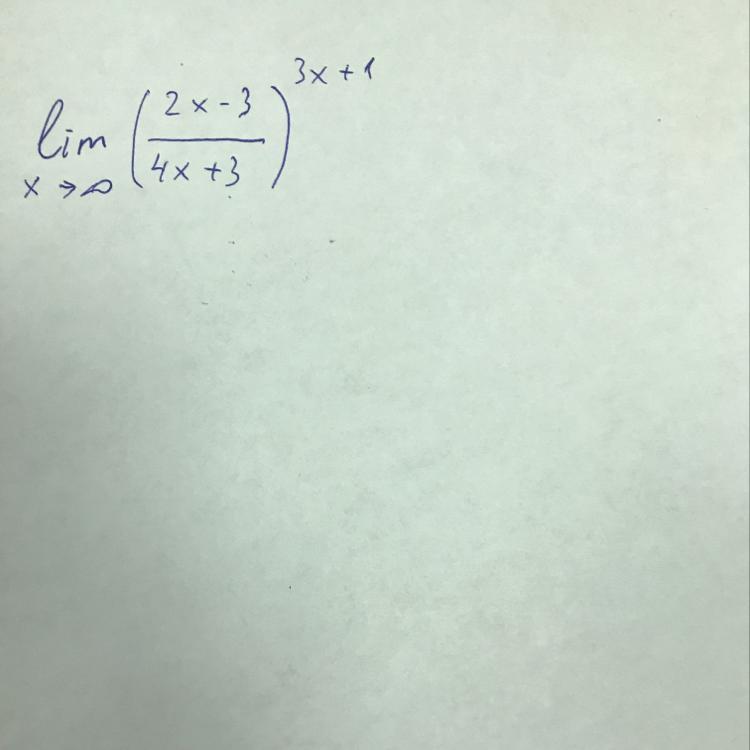Ответы
Ответ дал:
0
AhahaStudio:
можно проще и короче. просто вынести из числителя и знаменателя икс. тогда дробь = 1/2 при x --> 00. а степень дроби стремится к бесконечности. а 1/2 в степени бесконечность = 0 (в пределе, конечно)
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад