Question

В равнобедренной трапеции ABCD меньшее основание BC равно 5 см, боковая сторона — 4 см, а угол при основании равен —
60
∘
60∘. Найдите большее основание AD (в см).

Answer 1

Опустим два перпендикуляра BF и CF на большее основание. Получим два равных прямоугольных треугольника, так как трапеция равнобедренная, а так же EF=BC=5.

cos∠A=AE/AB→AE=AB•cos∠A=4•cos60º=2

AD=AE+EF+FD=2+5+2=9

ответ на картинке лучшее

если я вам помог то поставьте 5 звёздочек заранее спасиба ;)

Answer 2

Ответ:

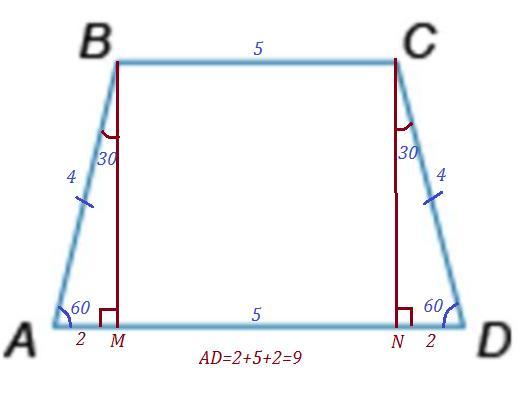
АВСD - трапеция  , АВ=СD=4 , ВС=5 , ∠А=∠D=60°

Опустим перпендикуляры  ВМ⊥AD  ,  CN⊥AD  ⇒ΔABM  и ΔCDN - прямоугольные и равные (АВ=CD , ∠A=∠D , BM=CN  по 1-му признаку )

∠ABM=∠DCN=90°-60°=30°

Против угла в 30° лежит катет, равный половине гипотенузы  ⇒

АМ=ND=4:2=2

BCNM - прямоугольник , тогда BС=MN=5 .

AD=AM+MN+ND=2+5+2=9