Question

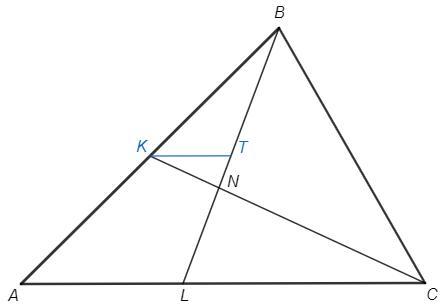
в треугольнике ABC точка K — середина отрезка AB. Точка L принадлежит АС, причем AL=4 LC=6. отрезки CK BLпересекаются в точке N найдите KN:NC

Answer 1

По теореме Менелая

AL/LC *CN/NK *KB/BA =1

4/6 *CN/NK *1/2 =1 <=> NK/CN =1/3

Докажем. Пусть KT||AC.

KBT~ABL, KB/AB=KT/AL

KNT~CNL, KN/CN=KT/CL

Приравняем по KT

KB/AB *AL =KN/CN *CL <=>  KB/AB *AL/CL *CN/KN =1