Question

  ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!!

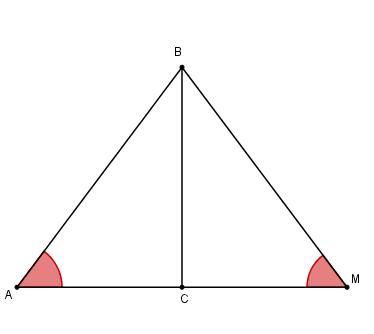
В равнобедренном треугольнике АВМ высота ВС = 16 см, а боковая сторона относится к основанию АМ как 5 : 6. Найдите периметр и площадь треугольника АВМ.​

Answer 1

Пусть коэффициент пропорциональности равен х, тогда AB = 5x см и AM = 6x см и так как BC - высота, медиана и биссектриса, то AC = AM/2 = 3x см. По теореме Пифагора из прямоугольного треугольника ABC

$(5x)^2=(3x)^2+16^2\\ \\25x^2=9x^2+16^2\\ \\ 25x^2-9x^2=16^2\\ \\ 16x^2=16^2\\ \\ x^2=16\\ \\ x=4$

Следовательно, AB = BM = 5 * 4 = 20 см и AM = 6 * 4 = 24 см

P(ABM) = AB + BM + AM = 20 + 20 + 24 = 64 см

S(ABM) = 0.5 * BC * AM = 0.5 * 16 * 24 = 512 см²