Question

2COS^(4)4X-COS4X-3=0
РЕШИТЕ УРАВНЕНИЕ

Answer 1

Ответ: x=pi/4+pik/2

Пошаговое объяснение: на фото.

Answer 2

2cos⁴4x - cos4x - 3 = 0

2cos⁴4x = cos4x + 3

Пусть cos4x = t, t ∈ [ - 1 ; 1 ], тогда

2t⁴ = t + 3

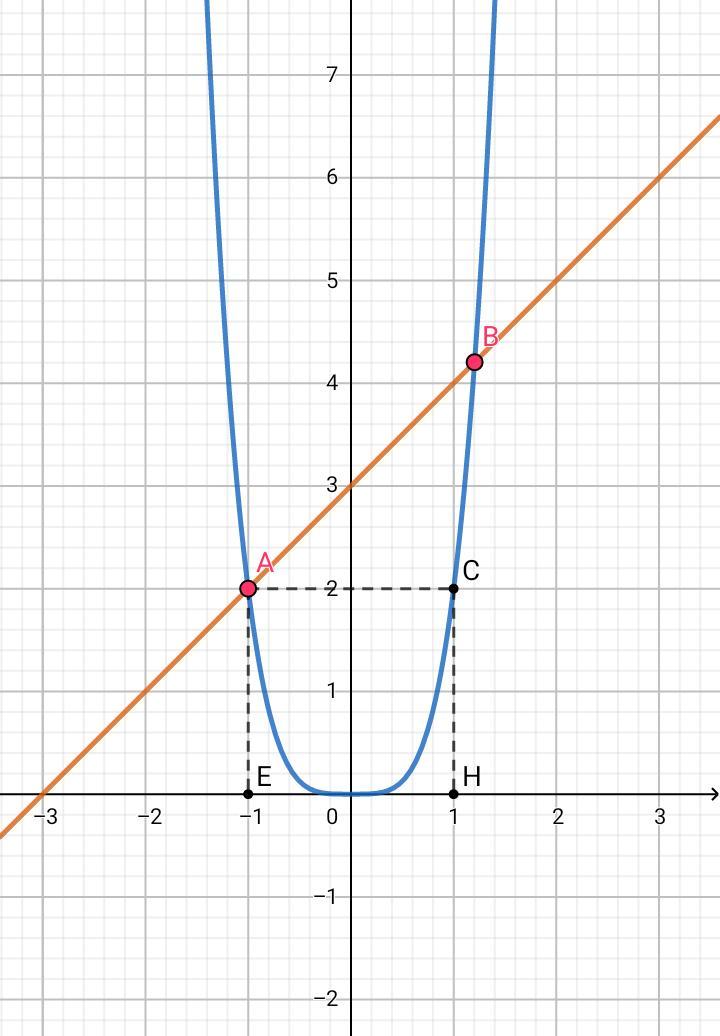
Нарисуем графики функций обеих частей уравнения:

• f(t) = 2t⁴ - синий график, чётная функция, симметричен относительно оси ординат, при t => - ∞ и + ∞ , f(t) => + ∞
• g(t) = t + 3 - оранжевый график, линейная функция, возрастающая

Графики функций пересекаются в 2 точках: А и В.

Первый корень несложно найти, t₁ = - 1 ⇒ f(t₁) = 2. Если построить точку А (-1;2) симметрично, относительно оси ординат, то попадаем в точку t₀ = С (1;2). График функции f(t) при t ≥ 0 возрастает, поэтому f(t₂) > f(t₀) ⇒ t₂ > t₀  ⇒ t₂ > 1 , но t ∈ [ - 1 ; 1 ] ⇒ ∅

t = - 1 ⇔ cos4x = - 1 ⇔ 4x = π + 2πn ⇔ x = (π/4) + (πn/2), n ∈ Z

Ответ: (π/4) + (πn/2), n ∈ Z