СРОЧНО!
ПОМОГИТЕ ПОЖАЛУЙСТА,НЕ МОГУ ПОНЯТЬ ЧТО К ЧЕМУ,И КАК ЭТО РЕШАТЬ
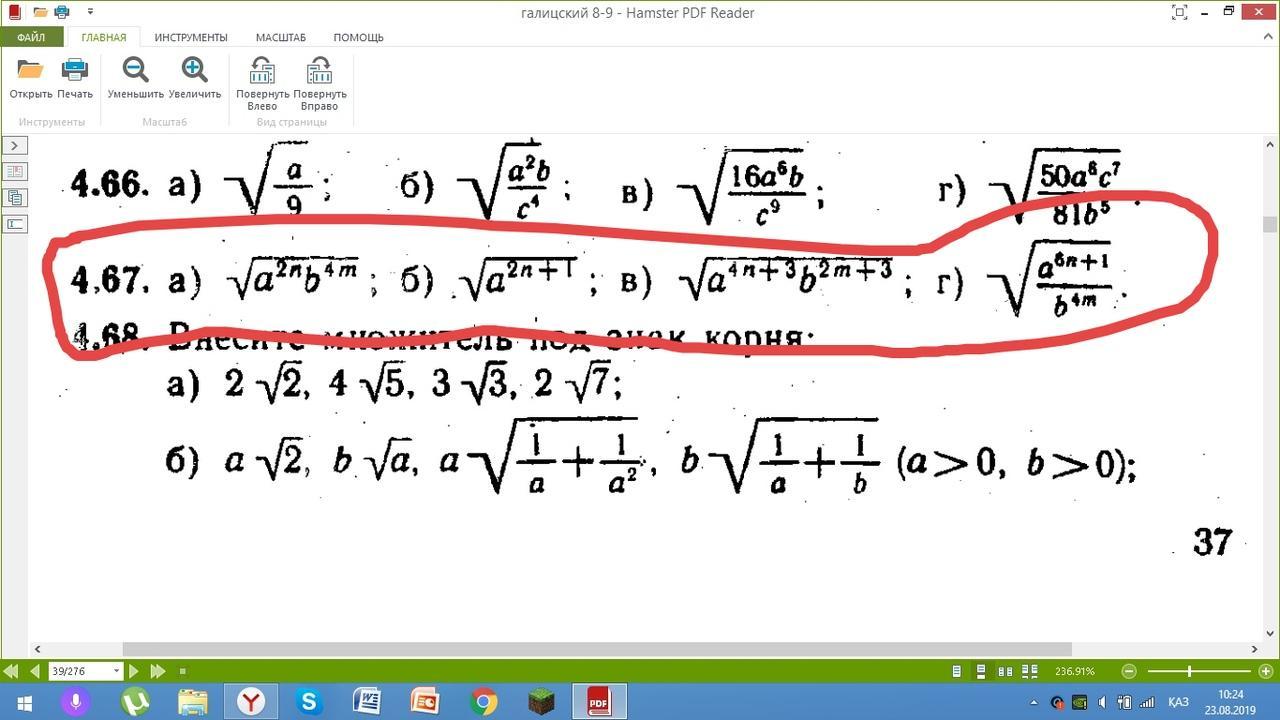
задача 4.67
Приложения:
elyalevitan:
а решать то чтр
задачу под номером 4.67
Ответы
Ответ дал:
1
№4.67
а)
б)
в)
г)
неверно... здесь модуль должен присутствовать) под а) переменная (а) может принимать отрицательные значения...
спасибо большое
там вроде должен присутствовать модуль,ибо как ты и сказал/а а может принимать отрицательные значения.Потому что ничего не дано
Ответ дал:
0
Формула:
Объяснение:
опечатка: в 3) извлечется |a^2n| и b^m останется под модулем...
и в 1) знак "минус" будет зависеть еще от четности n, т.е. будет не всегда)) лучше закончить решение на выражении с модулем (не расписывать)
Спасибо, исправила.
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
9 лет назад