Ответы
Ответ дал:
1
Доказательство:
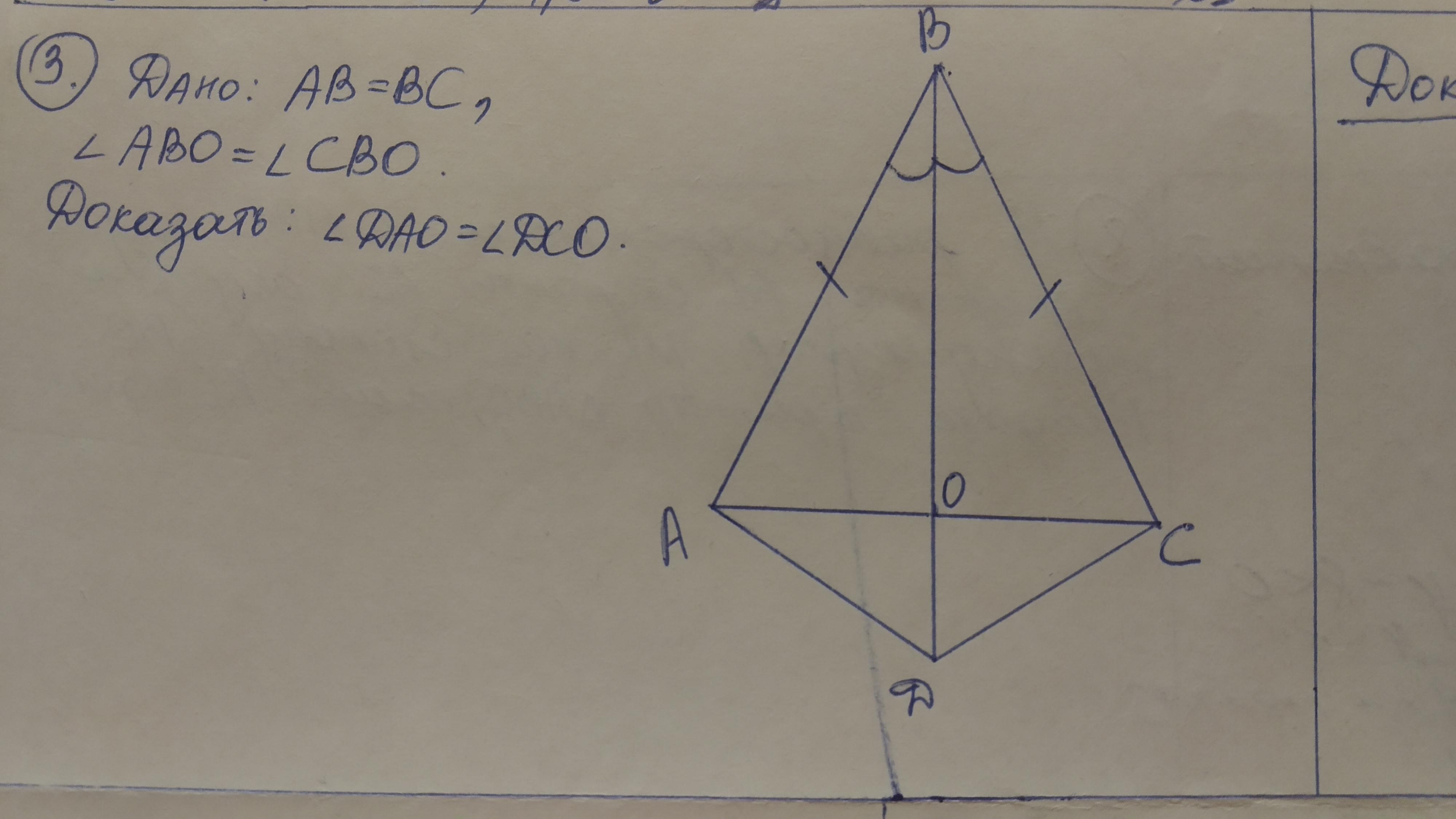
Заметим, что ΔAOB = ΔBOC (по первому признаку равенства: AB = BC по условию, BO общая сторона, ∠ABO = ∠CBO, по двум сторонам и углу между ними). Из этого следует так же равенство AO = CO, и соответственно равенство углов ∠AOB = ∠BOC (более того, каждый равен по 90°: так как они смежные, то в сумме должны давать 180 градусов, с другой стороны, углы равные, а это возможно только при углах в 90°). Поэтому ∠AOD = ∠DOC = 90°. Треугольники ADO и DOC равны по первому признаку равенства: AO = OC как следствие равенства треугольников ABO = BOC, DO - общая сторона, и ∠AOD = ∠DOC. Это и означает равенство углов ∠DAO = ∠DCO, что требовалось доказать.
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
8 лет назад