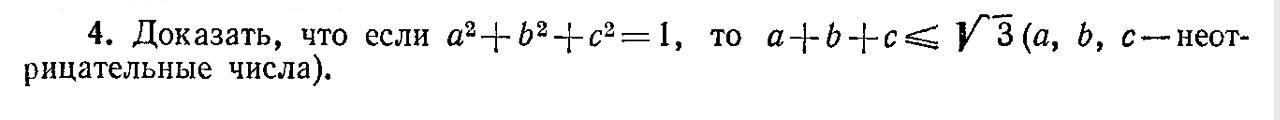Ответы
Ответ дал:
1
Доказательство:
По неравенству Коши мы знаем, что среднее арифметическое не превышает среднее квадратичное, то есть выполняется следующее неравенство при неотрицательных a, b и с:
Так как , то имеем неравенство:
, что и требовалось доказать
000LeShKa000:
кстати, интересный факт: неравенство превращается в уравнение a + b + c = sqrt(3), тогда и только тогда, когда a = b = c
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
8 лет назад