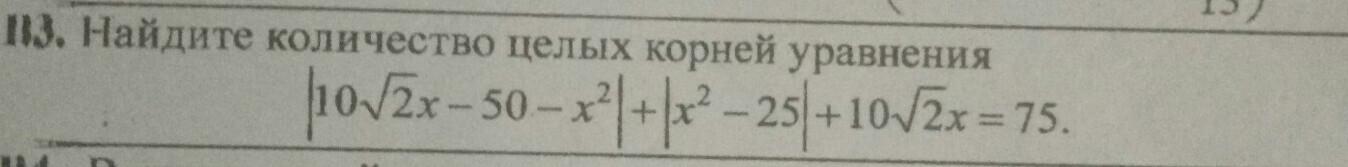Ответы
Ответ дал:
1
|10√2х - 50 - х²| + |х² - 25| + 10√2х = 75
- - х² + 10√2х - 50 = - (х² - 10√2х + 50) = - (х - 5√2)²
| - (х - 5√2)² | + |х² - 25| + 10√2х = 75
(х - 5√2)² + |х² - 25| + 10√2х = 75
х² - 10√2х + 50 + |х² - 25| + 10√2х = 75
|х² - 25| = - х² + 25
Равенство достигается только тогда, когда х² - 25 ≤ 0 ⇔
⇔ (х - 5)(х + 5) ≤ 0 ⇔ х ∈ [ - 5 ; 5 ]
Количество целых корней данного уравнения - 11 ( - 5 ; - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 ; 5 )
Ответ: 11
Аноним:
Когда в уравнении присутствуют модули, то большая вероятность, что ответом будет не один/несколько корней, а промежуток.
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад