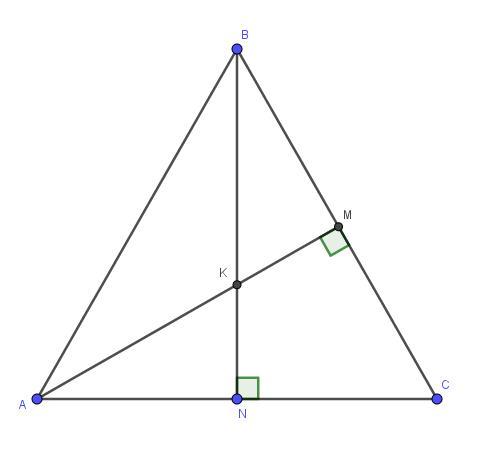
В треугольнике АВС (АВ = ВС) проведены высоты BN и АМ, причем BN пересекает АМ в точке К.
а) Докажите, что треугольники АМС и BNC подобны.
б) Найдите коэффициент подобия указанных треугольников, если <ABC=120°.
Ответы
Ответ дал:
3
1) У треугольников AMC и BNC — общий и ∠BNC = ∠AMC, следовательно, ΔAMC ~ ΔBNC по двум углам.
2) Поскольку BN - высота, медиана и биссектриса, то
Коэффициент подобия:
Приложения:
pand53:
спасибо большое
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад