У трикутнику АВС точка М середина ВС, АС 24 см знайдіть відстань d від точки М до сторони АС, якщо площа трикутника АВС 96 см^2
Ответы
Ответ дал:
8
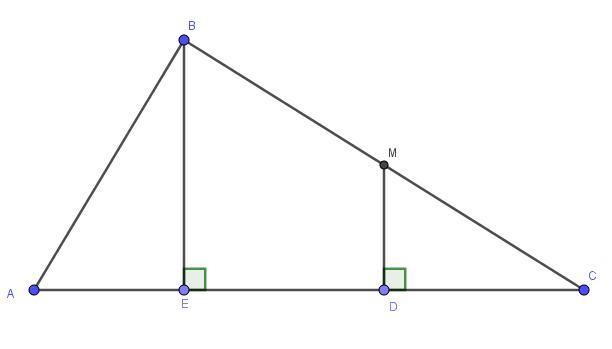
Так как BE и MD перпендикулярны к одной прямой, то BE || MD
Поскольку M - середина, то MD - средняя линия треугольника BEC, по свойству средней линии треугольника
см
Ответ: 4 см.
Приложения:
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад