Question

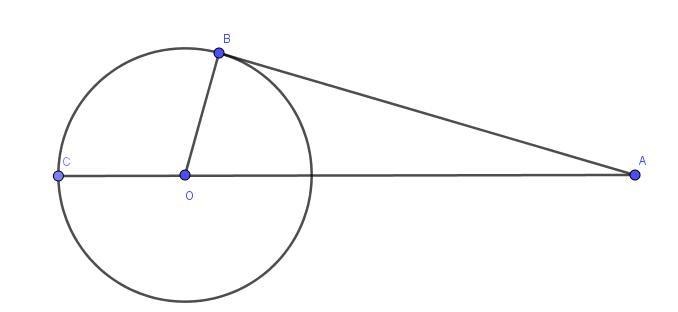
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB = 3.

Answer 1

Радиус окружности, проведённый в точку касания, перпендикулярен касательной, т.е. ∠OBA = 90°. Из прямоугольного треугольника AOB по теореме Пифагора

$AO=\sqrt{AB^2+OB^2}=\sqrt{3^2+\left(\frac{8}{2}\right)^2}=5$

Тогда AC = OC + OA = (8/2) + 5 = 4 + 5 = 9

Ответ: 9.