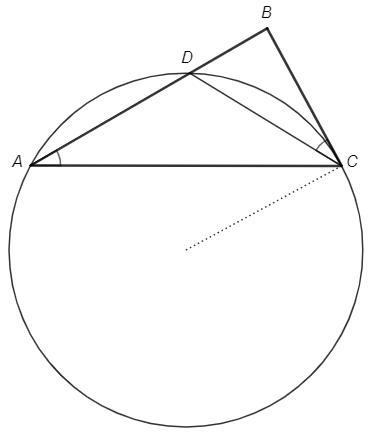
Через вершины A и C треугольника ABC проходит окружность, пересекающая сторону AB в точке D и касающаяся стороны BC. Найдите AD, если AC=8,BC=4,DC=8/√3.
Аноним:
Отмечу, что это задание уже есть на сайте, и главный мозг уже отвечал на него.
Можно для нахождения АD воспользоваться теоремой о касательной и секущей. || Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: ВС²=АВ•BD.|| Ответ получится тот же, но решение будет длиннее. А, как известно, лучшим является более короткое и простое решение.
Действительно :) Второй раз.
Тогда другое решение. Треугольники ABC и CBD подобны. Видим, что стороны в них относятся как 1:V3:2 - треугольники с углами 30, 60. Значит углы при основании ADC равны. AD=DC.
Ответы
Ответ дал:
1
Угол между касательной (BC) и хордой (CD) равен половине дуги, стягиваемой хордой.
Вписанный угол равен половине дуги, на которую опирается.
∠BCD=∪CD/2=∠CAD
△ABC~△CBD (по двум углам)
BC/BD =AC/CD <=> 4/BD =8√3/8 <=> BD=4/√3
AB/BC =BC/BD <=> AB/4 =4√3/4 <=> AB=4√3
AD=AB-BD =4√3 -4/√3 =8/√3
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад