Срочно, помогите пж
Точки A и B лежат вне квадрата PQRS, и при этом треугольники ARS и BQR равносторонние. Найдите угол APB.
akaman32:
60 градусов
Ответы
Ответ дал:
13
Ответ:
∠АРВ=60°
Объяснение:
Выполним дополнительные построения, соединив точки А, В, Р.
Докажем, что ΔАРВ - равносторонний.
Рассмотрим ΔPQB. Он равнобедренный с основанием РВ, т.к. PQ=QB. Угол, лежащий напротив основания ∠PQB=∠PQR+∠BQR=90+60=150°.
Аналогично ΔPSA с основанием РА - равнобедренный с ∠PSA=150°.
Рассмотрим ΔBRA. он равнобедренный с основанием ВА. т.к. BR=RA. В нем угол, лежащий против основания ∠BRA=360-∠BRQ-∠ARS-∠QRS=360-60-60-90=150°.
Тогда по двум сторонам и углу между ними
ΔPQB=ΔPSA=ΔBRA.
Следовательно и соответствующие стороны в них равны. А т.к. ΔАРВ образован основаниями равных равнобедренных треугольников, то он равносторонний.
Внутренние углы равностороннего треугольника равны 60°, значит ∠АРВ=60°.
Приложения:
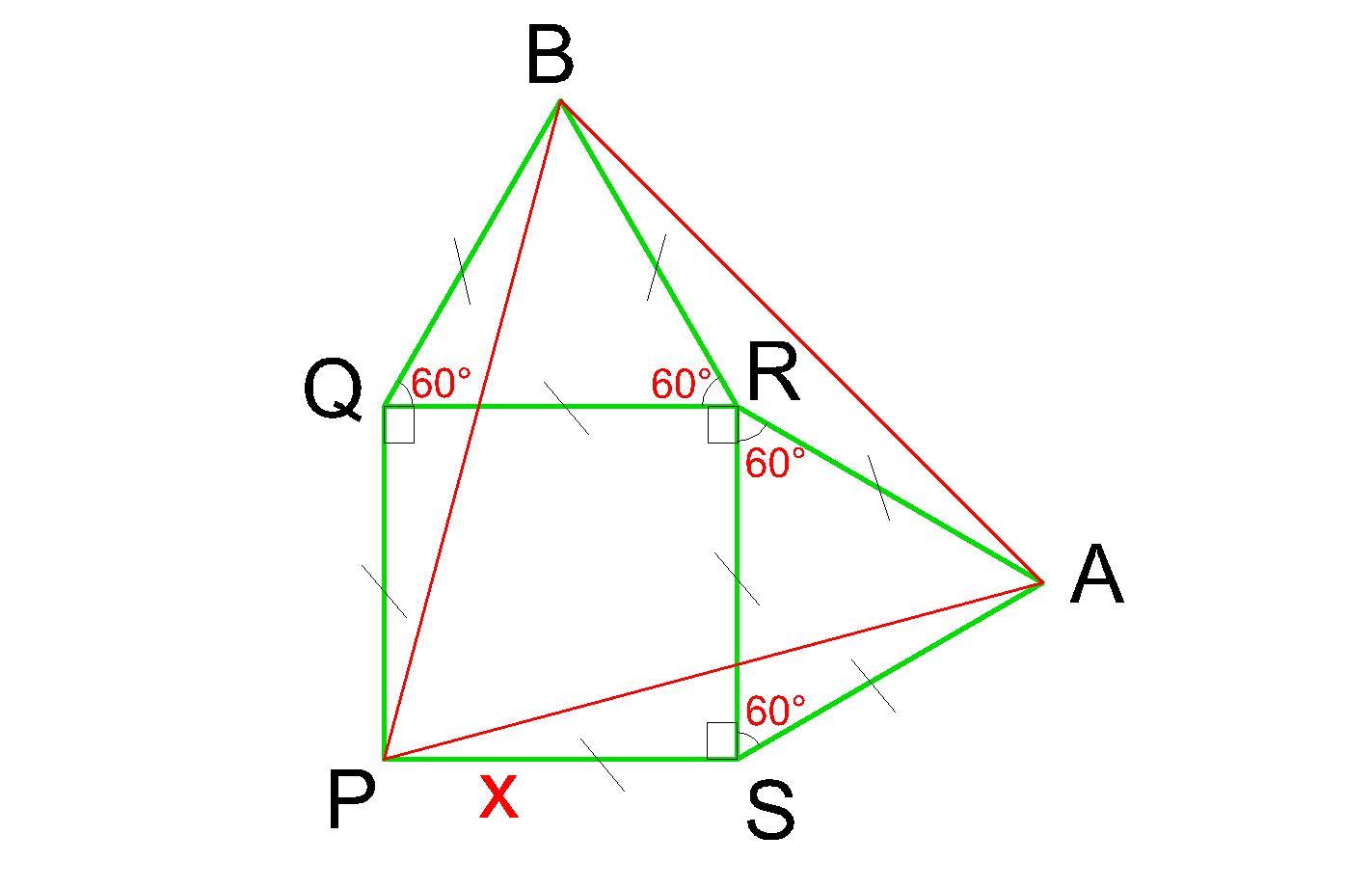
Как вариант, можно было высчитать углы при основании равнобедренных треугольников (15 градусов) и вычесть 2 таких угла из прямого угла. См. рисунок.
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
9 лет назад