Question

Помогите пожалуйста, это срочно!, заранее спасибо)​

Answer 1

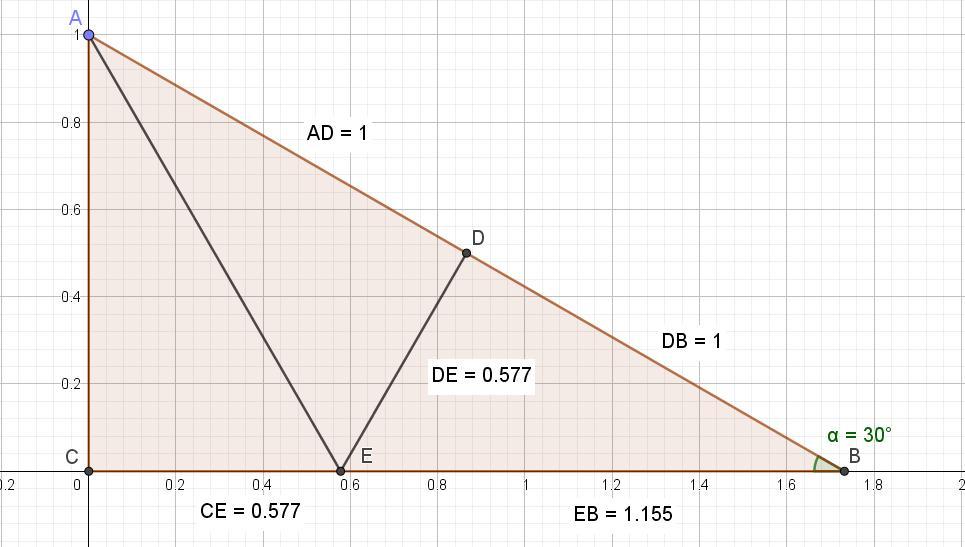
Пусть имеем прямоугольный треугольник АВС с прямым углом С и углом В = 30 градусов. Точка Д - середина гипотенузы.

Катет АС против угла 30 градусов равен половине гипотенузы.

При этом АС = АД.

ДЕ - отрезок перпендикуляра к гипотенузе через её середину.

Из равенства треугольников АСЕ и АДЕ (по двум сторонам и углу 90 градусов) следует равенство ДЕ = СЕ.

Из треугольника ВДЕ следует ВЕ = 2ДЕ (свойство угла 30°).

Получаем доказательство: ВС = 3ДЕ.