диагонали перпендикулярны, а основания 2см и 4 см. Найдите площадь равнобедренной трапеции
Аноним:
задай свой вопрос на сайте иркмикс.топ отвечает сама администрация
серьезно
Ответы
Ответ дал:
15
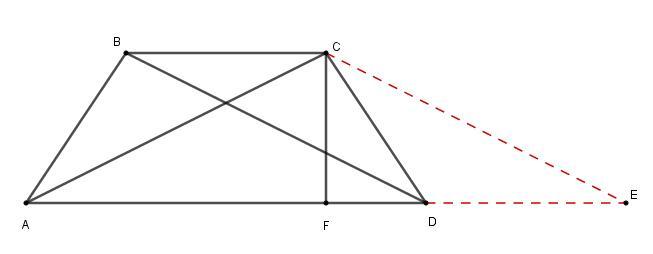
По условию, диагонали трапеции перпендикулярны. Из вершины проведём прямую параллельную диагонали
до пересечения на продлении прямой
за точку
. Имеем прямоугольный треугольник
, но так как трапеции равнобедренная, то ее диагонали равны, т.е.
, следовательно,
равнобедренный прямоугольный треугольник.
см, тогда
см.
Площадь прямоугольного треугольника см², с другой стороны она равна площади равнобедренной трапеции.
Ответ: 9 см²
Приложения:
AC=CE=AE/корень равно 3корнеь2, а откуда корень 2 взялась?
я же написал что равнобедренный прямоугольный треугольник. У него острые углы 45 градусов. По синусу или косинусу можете найти
большое спасибо
можете помочь с ещё одним заданием?
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад