Question

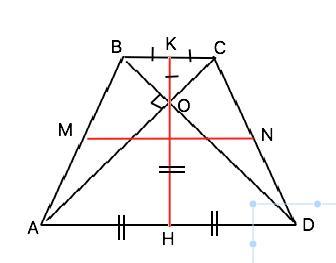
Задача по геометрии. Равнобедренная трапеция. Диагонали перпендикулярны друг другу. MN- средняя линия=10 см. Найти площадь трапеции

Answer 1

Ответ: 100 см²

Объяснение: Диагонали равнобедренной трапеции, пересекающиеся под прямым углом, образуют с основаниями равнобедренные прямоугольные треугольники BOC и АОD. Высота равнобедренного прямоугольного треугольника является его медианой и биссектрисой и равна половине гипотенузы. КО=ВК=КС; ОН=АН=HD.

 Высота трапеции равна сумме высот этих треугольников. значит, равна полусумме оснований, т.е.  средней линии. КН=0,5•ВС+0,5•АD⇒

КН=MN=10 см

Площадь трапеции равна произведению полусуммы оснований на высоту.  Ѕ=MN•H=10•10=100 см²