Ответы
Ответ дал:
0
Мы видим, что это формула разности квадратов, можно ее разложить по формуле: х² - 4у² = 5
(х -2у) · (х+2у) = 5
5 у нас число простое. Будем искать пары целых чисел, которые нам подойдут . Тогда рассмотрим все варианты,когда получится ответ 5, но будем использовать при подстановке только целые числа.
Если х = 3 и у = 1, то
3² - 4· 1² = 5
Потом, это пара чисел х = 3 и у = -1
3² - 4 (-1)² = 5
Еще одна пара чисел х = -3 и у = 1
(-3)² -4 *(1)² = 5
И последняя пара чисел х = -3 и у = - 1
(-3)² - 4 * (-1)² = 5
Больше целочисленных пар мы не найдем. Поэтому ответ будет таков,
(3; 1), (3; -1); (-3; 1); (-3; -1)
(х -2у) · (х+2у) = 5
5 у нас число простое. Будем искать пары целых чисел, которые нам подойдут . Тогда рассмотрим все варианты,когда получится ответ 5, но будем использовать при подстановке только целые числа.
Если х = 3 и у = 1, то
3² - 4· 1² = 5
Потом, это пара чисел х = 3 и у = -1
3² - 4 (-1)² = 5
Еще одна пара чисел х = -3 и у = 1
(-3)² -4 *(1)² = 5
И последняя пара чисел х = -3 и у = - 1
(-3)² - 4 * (-1)² = 5
Больше целочисленных пар мы не найдем. Поэтому ответ будет таков,
(3; 1), (3; -1); (-3; 1); (-3; -1)
Ответ дал:
0
Решение смотри в приложении
Приложения:
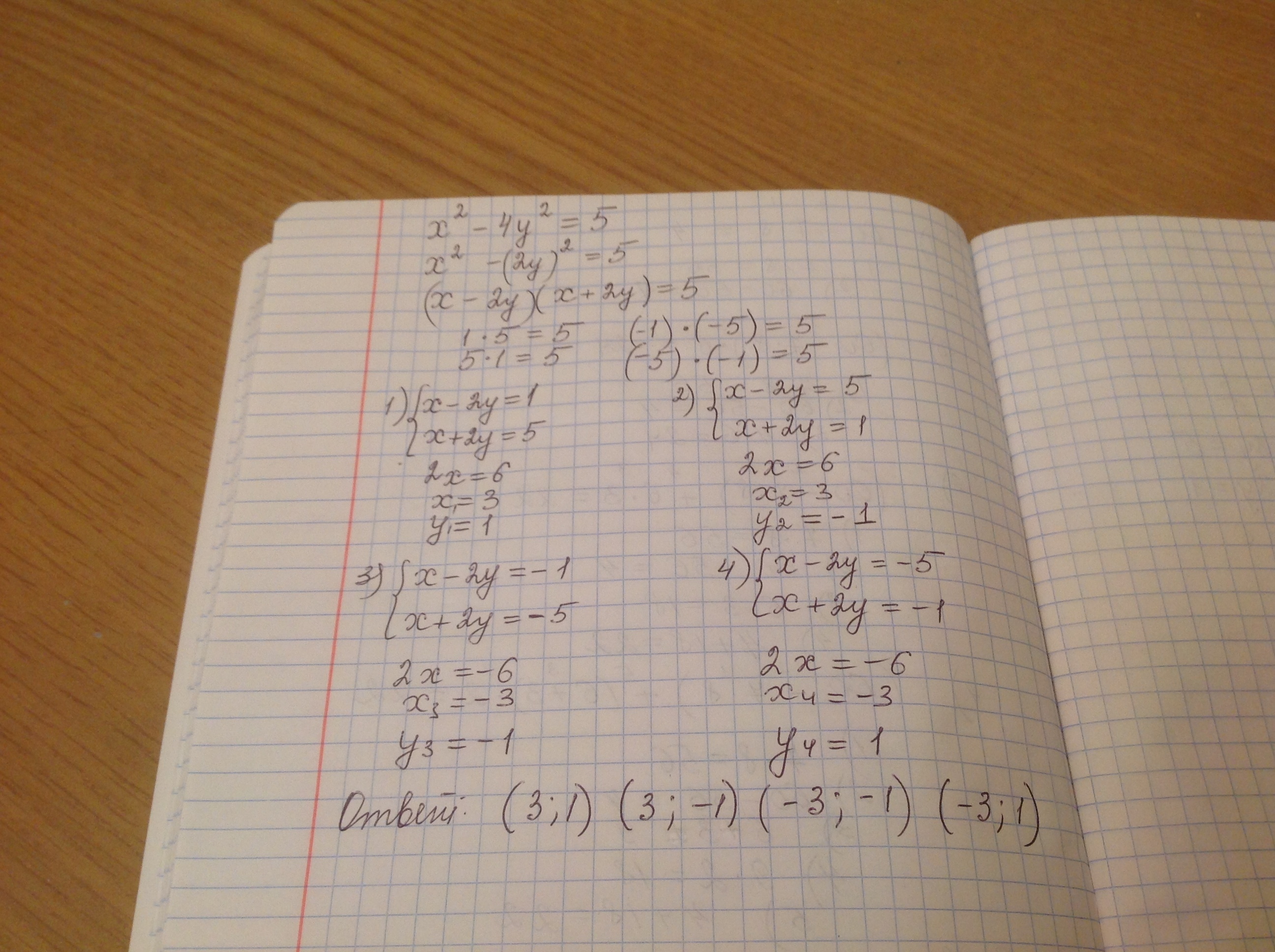
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад