Помогите решить производные.
Если не понятно, что на фото:
1. y=2ln3x
2. y=(1/3)*log(2)*4x
3. y=(x^2)/(2e^x)
4. y=(1/5)*cos2x
Приложения:
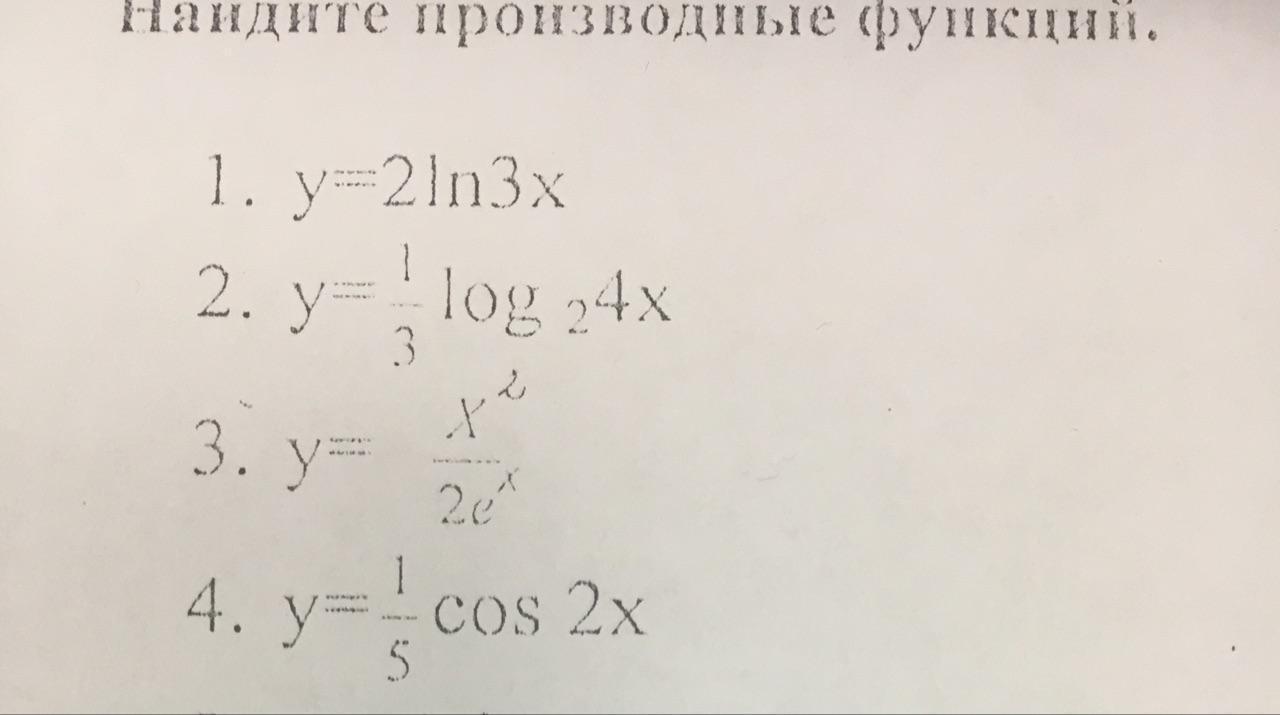
Ответы
Ответ дал:
1
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад