Помогите, пожалуйста. натуральные Числа номер 202 на фотке. нужно вывести? как можно решить это после соерщения? не просто калькулятором, а именно решением. спасибо заранее
Приложения:
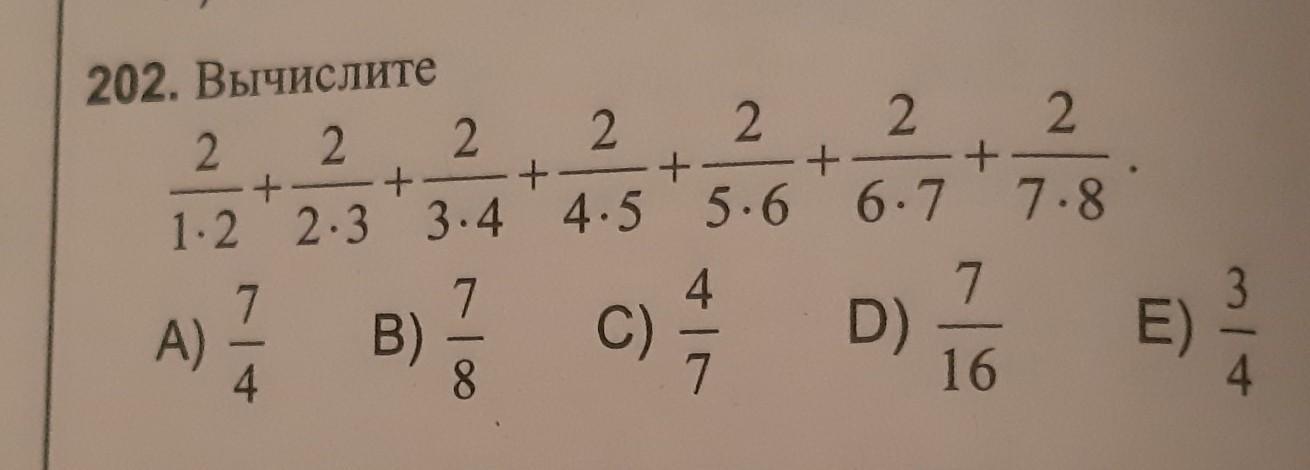
answer2020:
Решается через выведение формулы суммы ряда
Довольно незатейливо.
из пушки по воробью. Так легко считается.
1+2*((2+4)/(2*3*4)+(4+6)/(4*5*6)+(6+8)/(6*7*8))=1+2*(2/8+2/24+2/48)=1+2*(1/4+1/12+1/24)=
1+1/2+1/6+1/12=1+(6+2+1)/12=1 ¾=7/4
1+1/2+1/6+1/12=1+(6+2+1)/12=1 ¾=7/4
Да ладно, какой там из пушки по воробью. S(i)=i^2/(i*(i+1)/2) для i=7 получаем 49/28 = 7/4
я еще это не прошла, но спасибо большое обоим!
Да, там все просто. Выписываем несколько первых сумм и смотрим на получившуюся последовательность S(i): 1/1 ; 4/3 ; 9/6 ; 16/10. Сразу видим что в числителе i^2 , а в знаменателе сумма натурального ряда, вычисляемая по формуле i*(i+1)/2. Ставим вместо i число 7 и получаем искомый результат.
Заметить - не значит доказать.
Доказательства требуются при изучении сумм рядов, а не при их исследовании. Просто надо уметь различать стандартные последовательности в исследуемых.
Ответы
Ответ дал:
1
ответ А) 7/4 .......
Приложения:
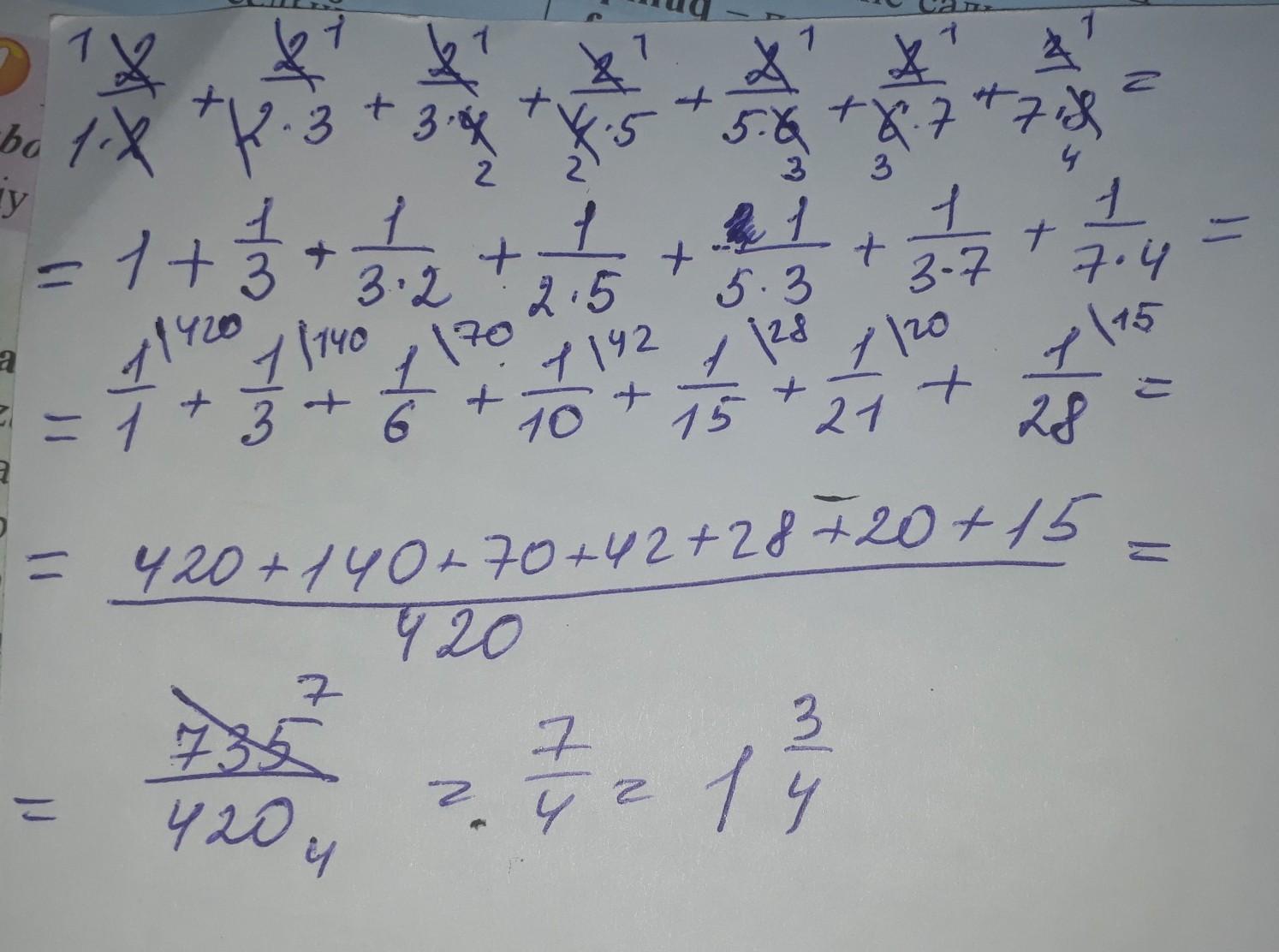
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад