Question

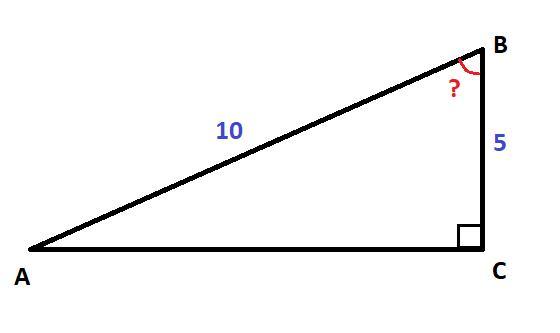
A9. В прямоугольном треугольнике гипотенуза равна 10 см, а один из катетов – 5 см.
Найдите наибольший из острых углов данного треугольника.
1) 90
2) 30
3) 60
4) 45​

Answer 1

Дано : ΔABC, ∠C = 90°, AB = 10 см,  BC = 5 см

Найти : ∠B

Решение :

Катет прямоугольного треугольника, лежащий напротив угла 30°, равен половине гипотенузы.

По условию гипотенуза AB вдвое больше катета BC

AB = BC·2 = 5·2 = 10 см  

⇒  Катет  BC лежит напротив угла 30° :  ∠А = 30°

Сумма острых углов прямоугольного треугольника равна 90°

⇒  ∠B = 90° - ∠A = 90° - 30° = 60°

∠B = 60°  >  ∠A = 30°

⇒   ∠B - наибольший острый угол ΔABC

Ответ : 3)  60°