Решить логарифмическое уравнение. Если это возможно, не используя метод замены переменной.
Приложения:
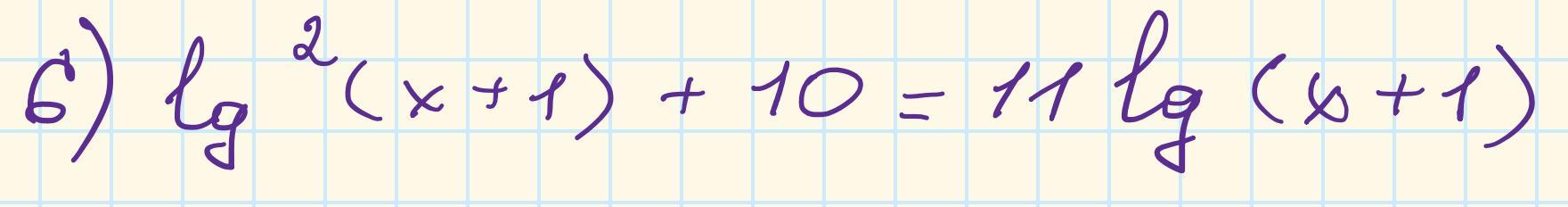
kirichekov:
это логарифмическое квадратное уравнение, замена переменной
Понял.
что за 2 в воздухе
Квадрат логарифма.
А без замены переменной никак? Там за скобки log можно вынести, перенеся всё в левую часть и приравняв нулю. Я ещё в процессе изучения и форсирую события. Скоро сам пойму думаю.
log(x+1)=a уравнение превращается в a^2+10=11a
Понял. Посмотрел повнимательней, действительно только методом замены решается. Ничего не получилось сократить. Всем спасибо. =)
Ответы
Ответ дал:
1
Ответ:
х1=9
х2=10^10-1
Объяснение:
ОДЗ: х+1>0, х>-1
логарифмическое квадратное уравнение, замена переменной:
D=81, t1=1, t2=10
обратная замена:
1). t1=1,
х+1=10
x=9. 9>-1, =>х =9 - корень уравнения
2). t2=10,
=> х=10^10-1 - корень уравнения
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад