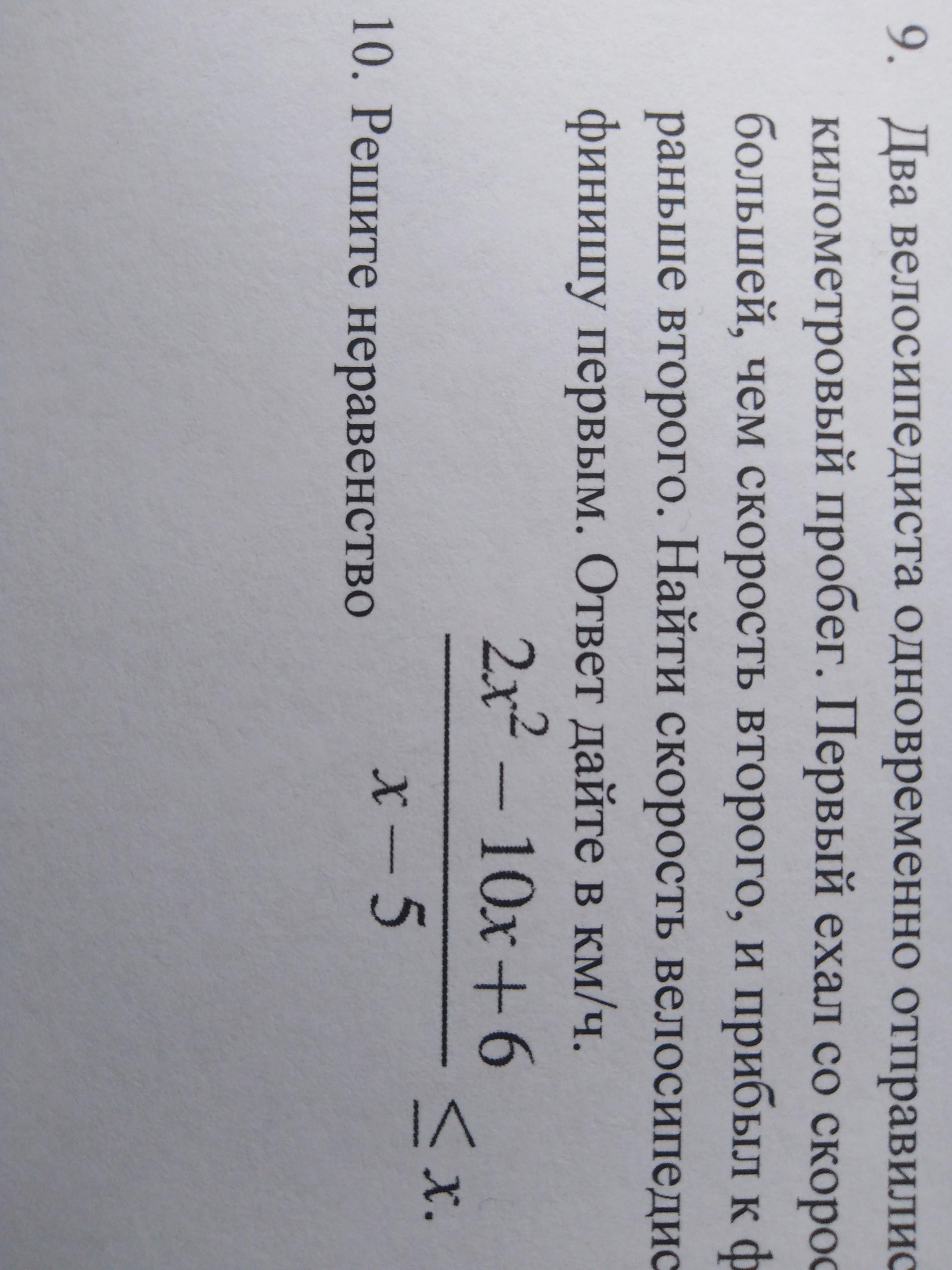Ответы
Ответ дал:
1
Ответ: x∈(-∞;2]∪[3;5).
Пошаговое объяснение:
Перенося x в левую часть, получаем неравенство (2*x²-10*x+6)/(x-5)-x≤0. Приводя левую часть к общему знаменателю x-5, получаем неравенство (x²-5*x+6)/(x-5)≤0. Так как x²-5*x+6=(x-2)*(x-3), то это неравенство принимает вид (x-2)*(x-3)/(x-5)≤0. А это неравенство будем решать методом интервалов.
1. Равенство (x-2)*(x-3)/(x-5)=0 возможно только при x=2 и при x=3.
2. Если x<2, то (x-2)*(x-3)/(x-5)<0.
3. Если 2<x<3, то (x-2)*(x-3)/(x-5)>0.
4. Если 3<x<5, то (x-2)*(x-3)/(x-5)<0.
5. Если x>5, то (x-2)*(x-3)/(x-5)>0.
6. Значение x=5 является недопустимым, так как при этом знаменатель дроби (x-2)*(x-3)/(x-5) обращается в 0.
Поэтому решением неравенства являются интервалы (-∞;2] и [3;5).
Vasily1975:
Решение готово.
Ошибся, сейчас исправлю решение и ответ.
Решение и ответ исправлены.
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад