Решите систему линейных уравнений методом Гаусса.Я решил его методом Крамера и получилось что:x=1,y=2,z=3.Преподователь сказал чтобы получить 4 нужно эту систему решить еще и Гауссом.Суть метода заключается в том чтобы ниже главной диагонали получились нули,но что то у меня совсем другие значения получаются в отличии от методом Крамера
Приложения:
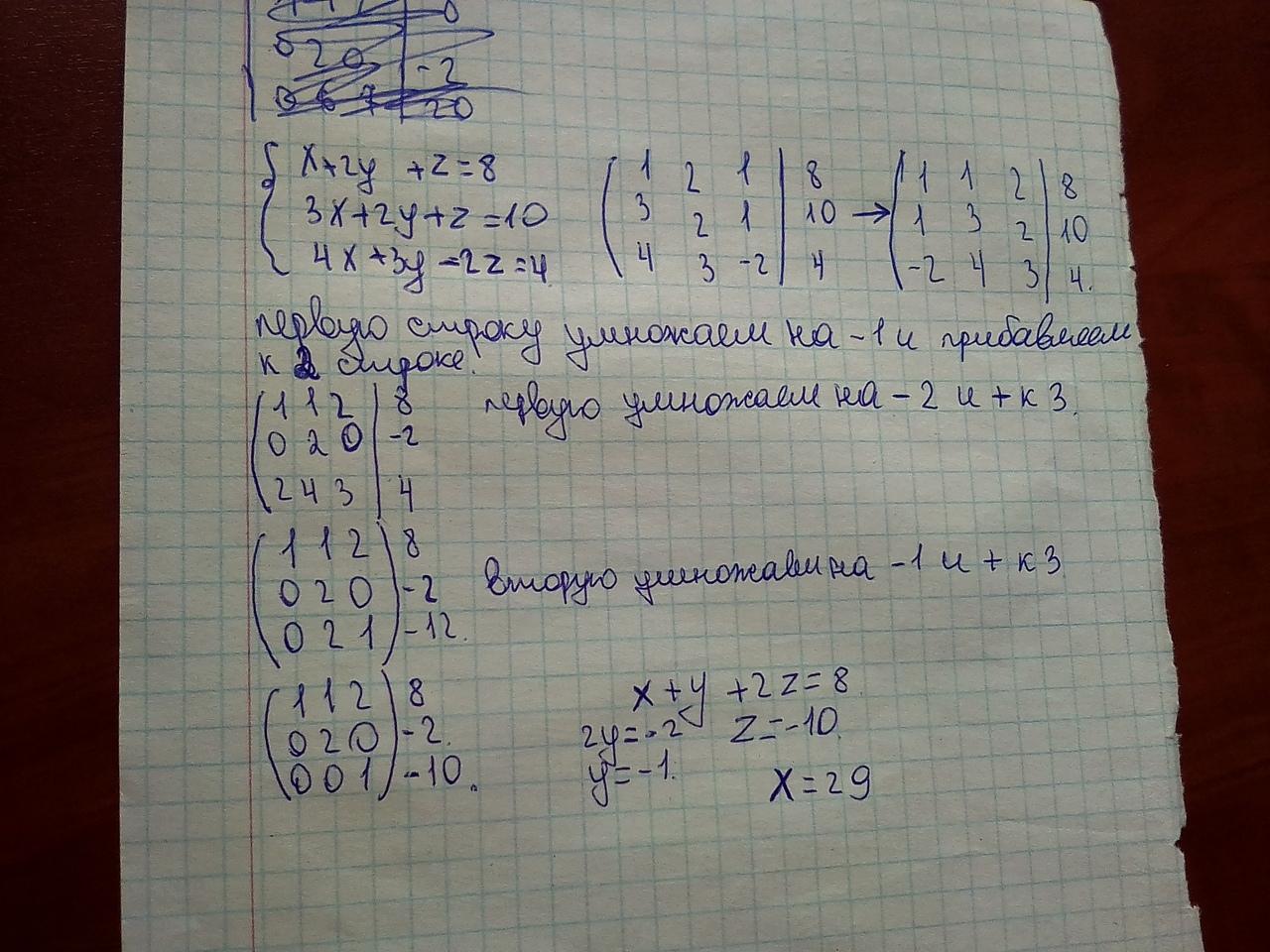
NNNLLL54:
при умножении 1 стр. на (-1) + 2 стр.= (0 2 0 | 2) , а у вас стоит (0 2 0 | -2) , а далее накапливаются вычислительные ошибки.
Ответы
Ответ дал:
1
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад