Найти производную данной функции и вычисить ее значение в данной точке х0?
а)f(x)= ; х0=3
; х0=3
б)f(x)= ;х0=
;х0=
Ответы
Ответ дал:
1
Аноним:
Спасибо
Ответ дал:
1
Ответ и решение во вложении
Приложения:
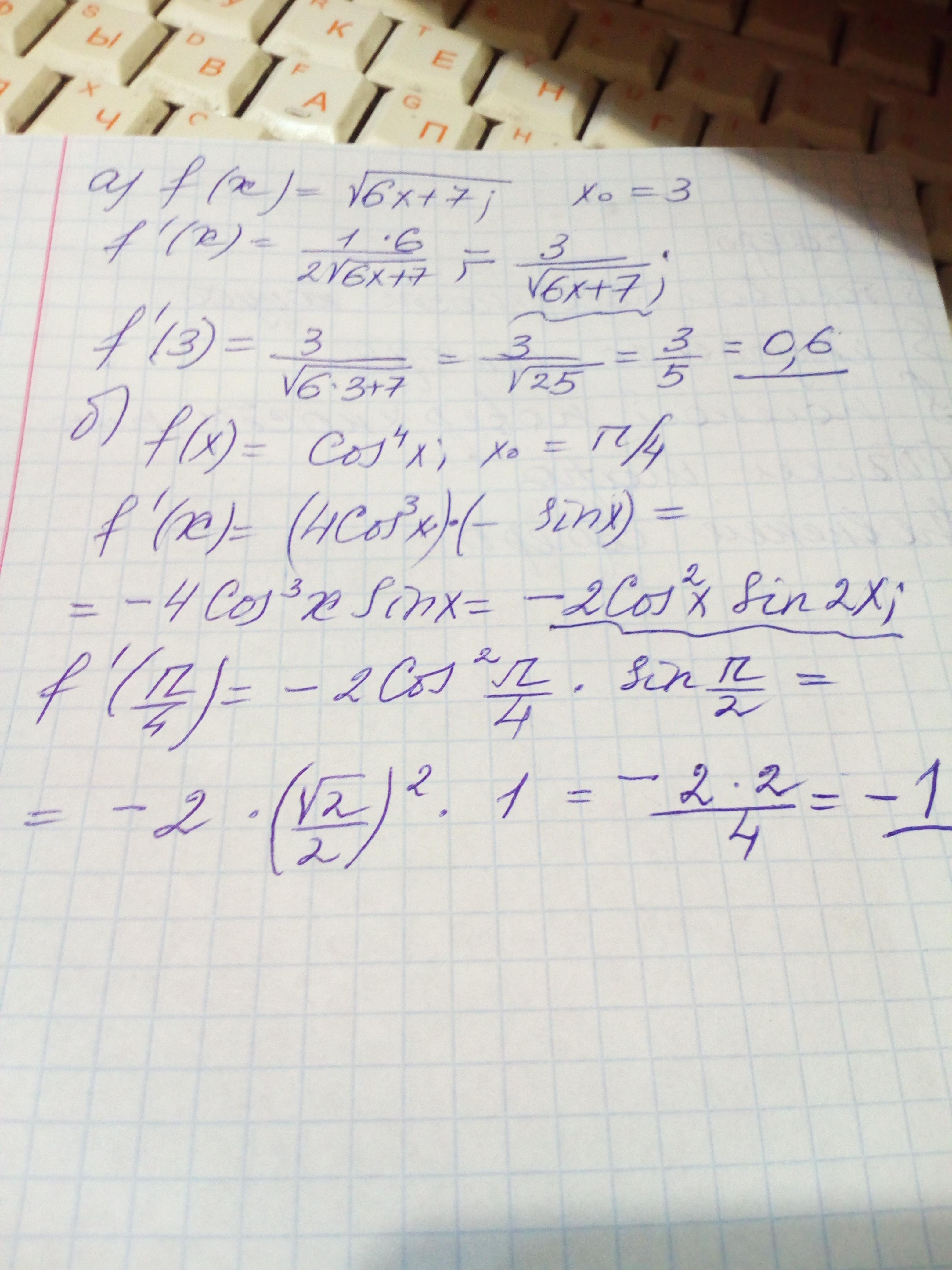
Спасибо
да не за что), обращайтесь
Подскажите пожалуйста, не могли бы Вы помочь с другими заданиями по алгебре? Я буду очень признательна)
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад