Ответы
Ответ дал:
1
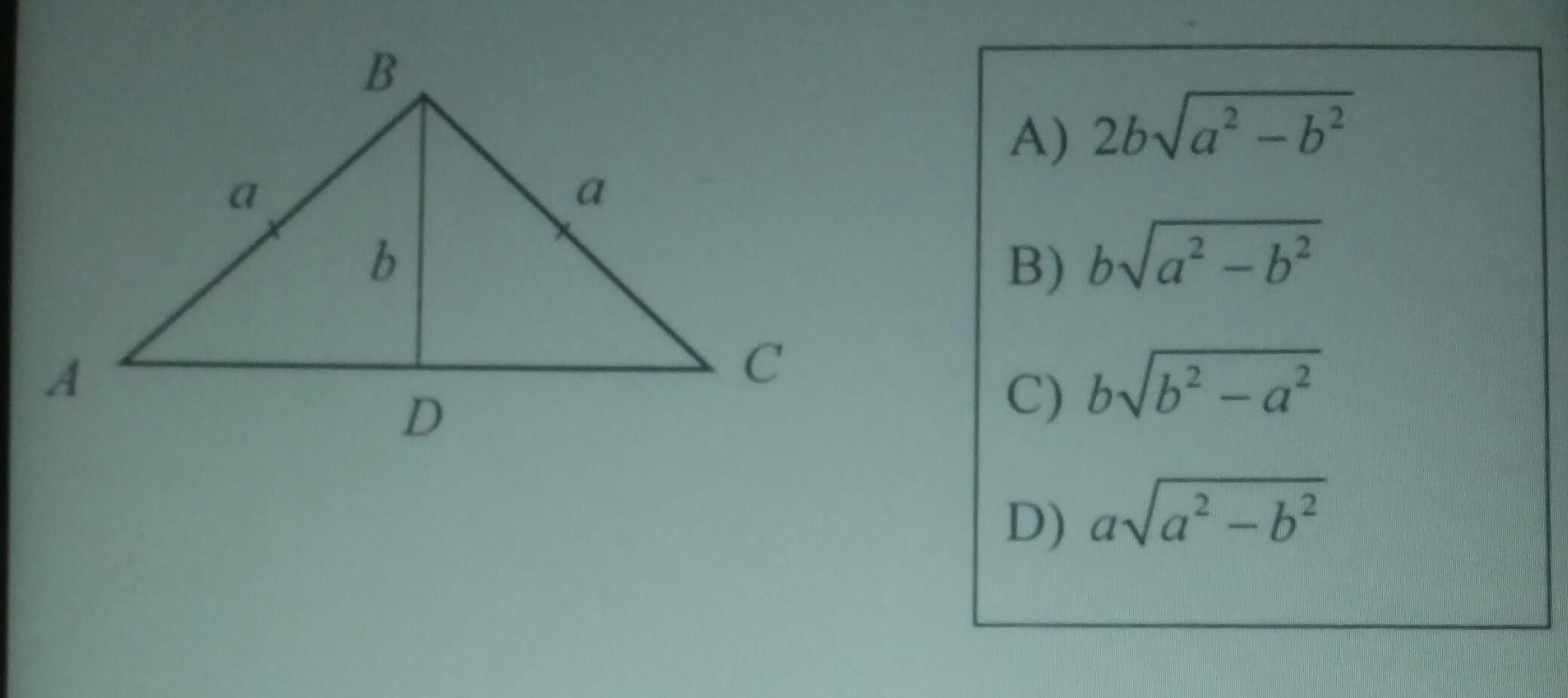
Из прямоугольного треугольника ABD по теореме Пифагора
Так как ВD - медиана равнобедренного треугольника, то
Ответ дал:
1
Т.к. ВD- высота, проведенная к основанию равнобедренного ΔАВС, то ВD- медиана, а, значит, площадь можем найти как ВD*АD, половину АС ищем из прямоугольного треугольника АВD, она равна
√а²-в², а площадь в*√(а²-в²)
vitusja1234:
https://znanija.com/task/33037034 помогите с заданием, пожалуйста
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
8 лет назад