((sin2x)/y + x)dx + (y - (sinx)^2/(y^2))dy =0
помогите решить уравнения в полных дифференциалах
Приложения:
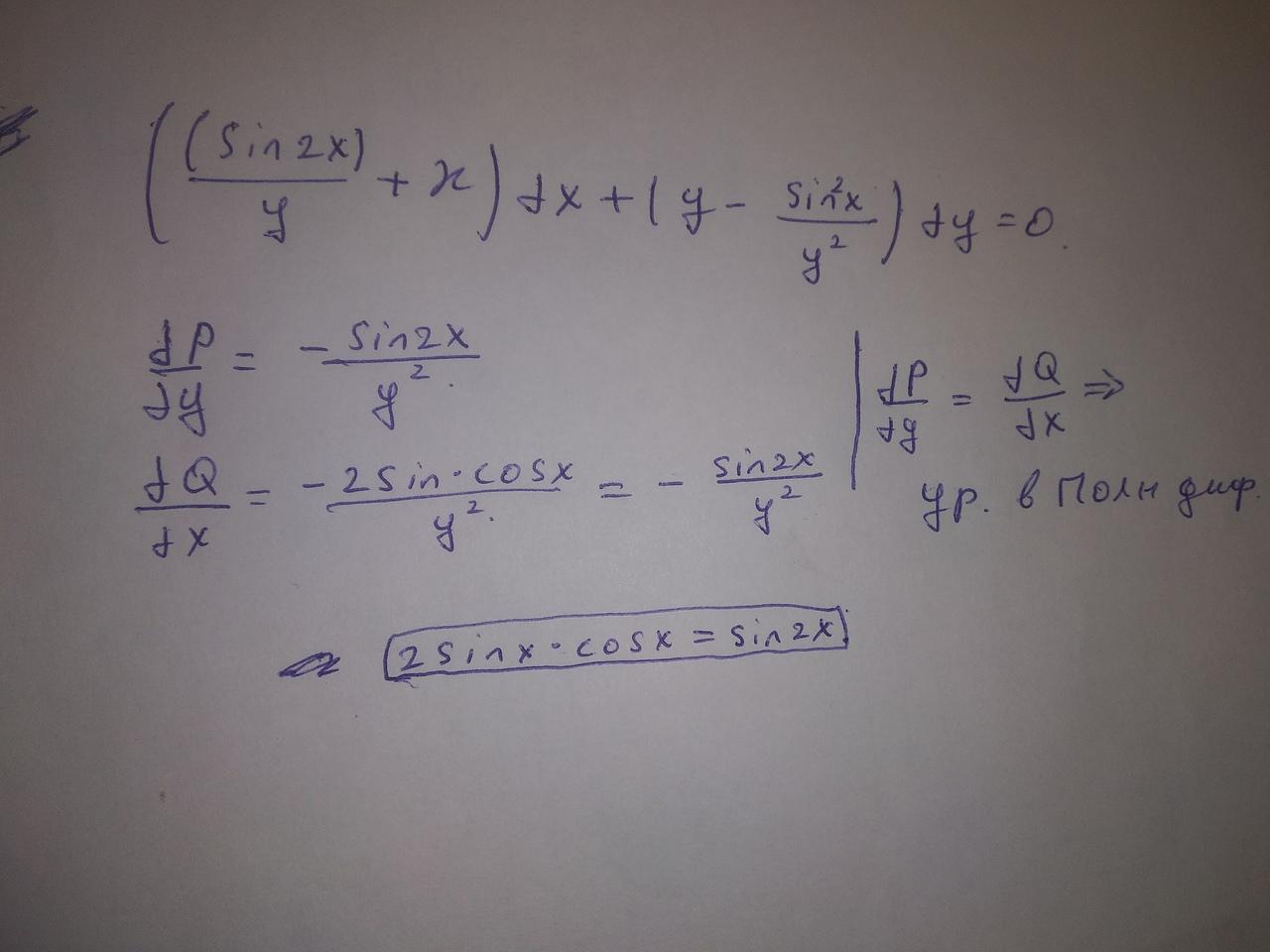

Аноним:
sin2x/y ? или sin2x/(y+x)
((sin2x/y)+x)dx
Диф. уравнение не является в полных дифференциалах
подскажите тогда, где я не прав?
dP/dy - почему минус перед?
Ну минуса там не должно быть, тогда равенство не выполняется.
(u/v)'=(u'*v-u*v')/V^2
Ну да, я не обратил внимания на знаменатель
Ответы
Ответ дал:
5
Уравнение является в полных дифференциалах, поскольку выполняется равенство
Если функция удовлетворяет
и
, то
- решение уравнения
Интегрируем функции F по переменной х
Далее дифференцируем по у
Действительно, . Отсюда
Общий интеграл
Решение поправил. Обновите страницу
слов нет, как благодарен)
На здоровье
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад