Ответы
Ответ дал:
0
Ответ:
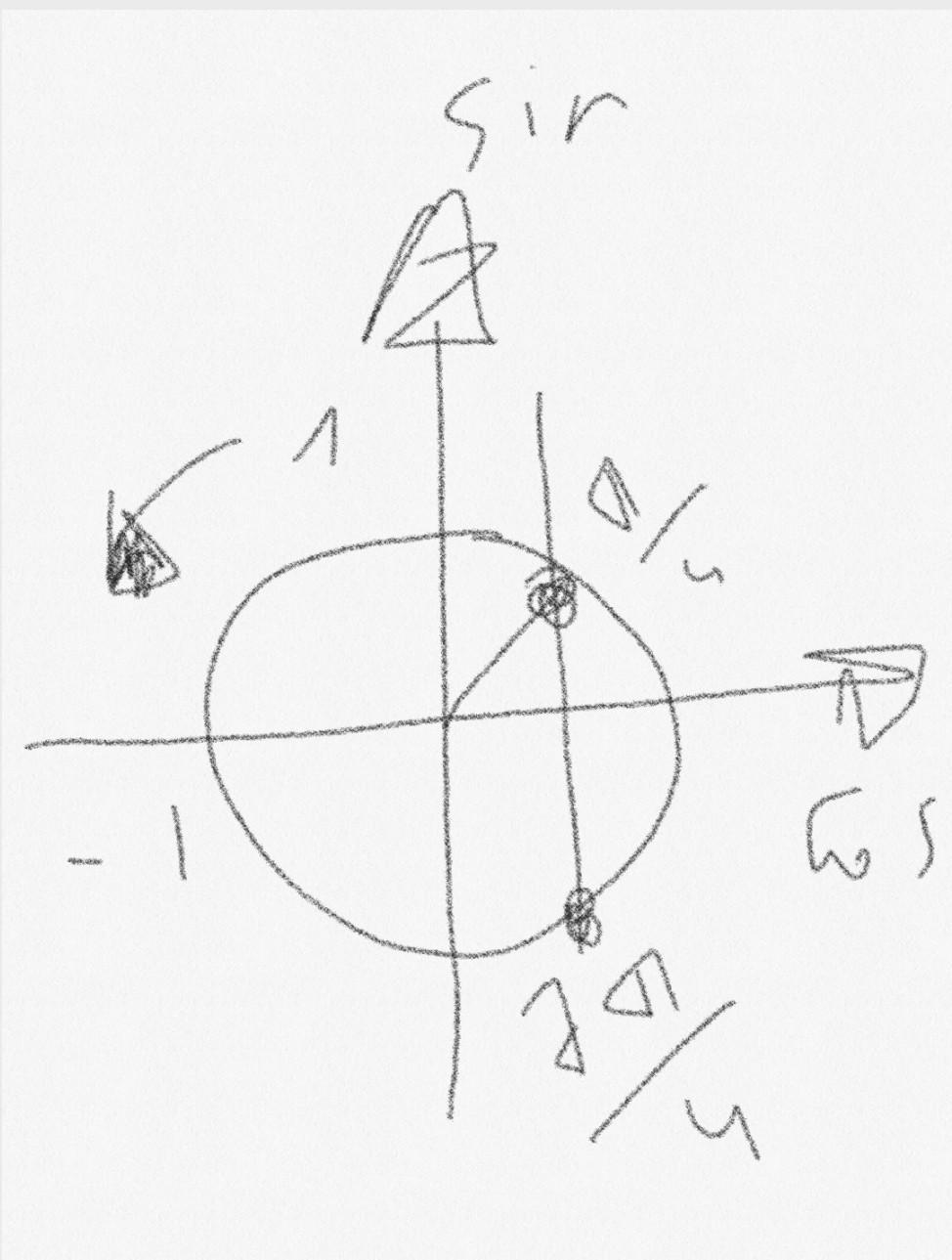
по единичной окружности, это дуга от
до
с периодом
но это для альфы, которая равна х/3 или
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад