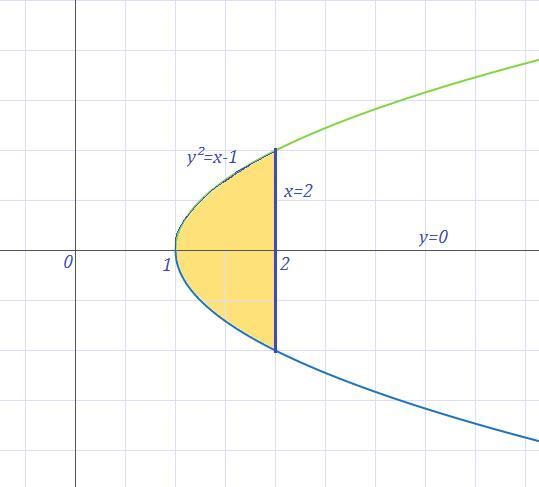
Найти объем тела, полученного при вращении вокруг оси абцисс фигуры, ограниченной линиями:
y^2-x+1=0 x-2=0 y=0
Ответы
Ответ дал:
0
Приложения:
Ответ дал:
0
Выразим х через у из формулы линии y²-x+1=0; у²(х)=(х-1); х= y²+1 Если у=0, то х=1, если же х-2=0, то х=2, пределы интегрирования 1 и 2.
Ищем объем тела по формуле /см. вложение /
Приложения:
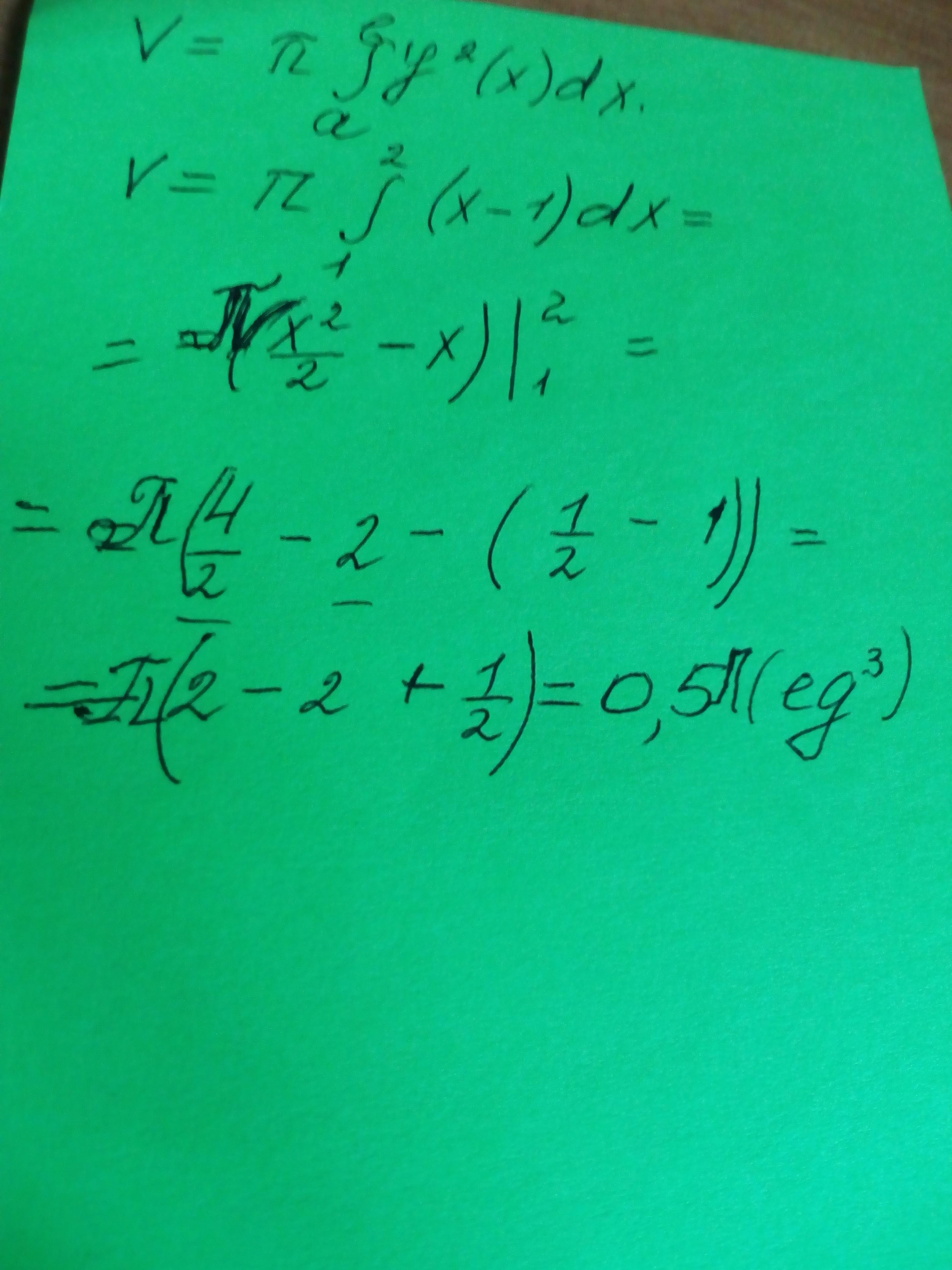
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад