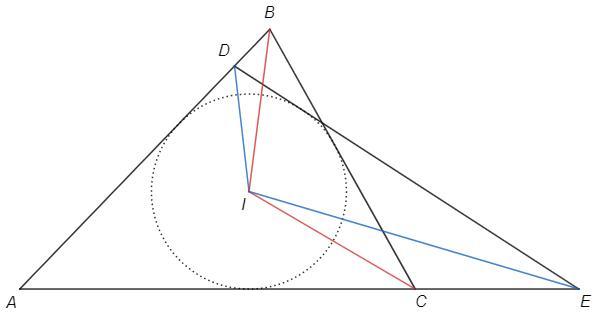
У треугольников ABC и ADE – общая
вписанная окружность с центром I (точка D лежит между точками A и B). Докажите, что угол BID равен углу CIE.
Ответы
Ответ дал:
6
Центр вписанной окружности лежит на пересечении биссектрис.
BI, CI- биссектрисы в △ABC
DI, EI - биссектрисы в△ADE
△ABC:
A/2 +B/2 +C/2 =90
BIC +B/2 +C/2 =180
BIC =90 +A/2 (задача об угле между биссектрисами)
Аналогично DIE =90 +A/2 (△ADE)
BIC=DIE => BID=CIE (из равных углов вычитаем BIE)
Приложения:
Вас заинтересует
2 года назад
3 года назад