На висоті AH1 гострокутного нерівнобедреного трикутника ABC з попарно різними сторонами вибрали деяку точку X , з якої на сторони AB та AC опустили перпендикуляри XN та XM відповідно. Виявилося, що H1A - бісектриса кута MH1N. Доведіть, що X - точка перетину висот трикутника ABC.
На высоте AH1 остроугольного неравнобедренного треугольника ABC с попарно различными сторонами выбрали некоторую точку X, с которой на стороны AB и AC опустили перпендикуляры XN и XM соответственно. Оказалось, что H1 - биссектриса угла MH1N. Докажите, что X - точка пересечения высот треугольника ABC.
Simba2017:
без перевода никак...
добавил перевод
откуда такая задача?
там получаются четырехугольники, вокруг которых можно описать окружности и через углы все получается доказать...
а можно с рисунком, с доказательством?)
я вам могу рисунок показать
лично я отталкивалась от другого вопроса
я построила точку пересечения высот Х и доказала равенство углов NH1X и XH1M
Ответы
Ответ дал:
1
////////////////////////////////////////////
Приложения:
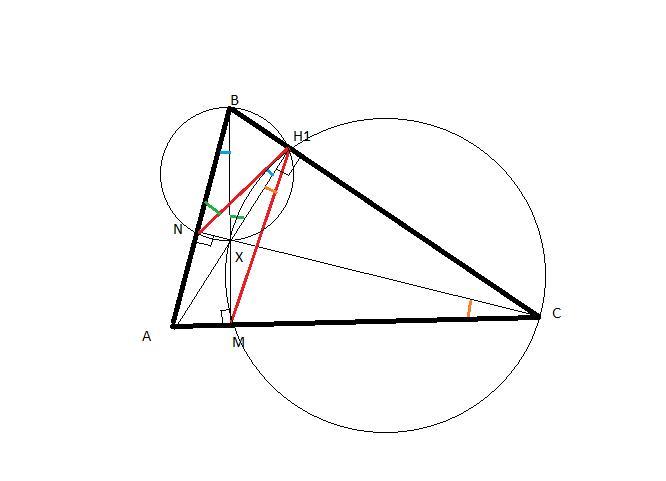
это понял. не понял только связь между равенством углов NH1X и XH1M с точкой X, как точкой пересечения высот
у вас в задаче оказалось что АН1- биссектриса и требуется доказать что Х-точка пересечения высот
я же решила обратную, я доказала равенство углов исходя из того, что Х-центр пересечение высот
это одно и тоже...
аа, теперь понял, спасибо
что еще неясно, просто через 40 минут я уже не смогу дополнить решение
теперь ясно, уже ничего не надо
хорошо, удачи)
здравствуйте,помогите пожалуйста с геометрией
будет очень хорошо ,если поможите
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад