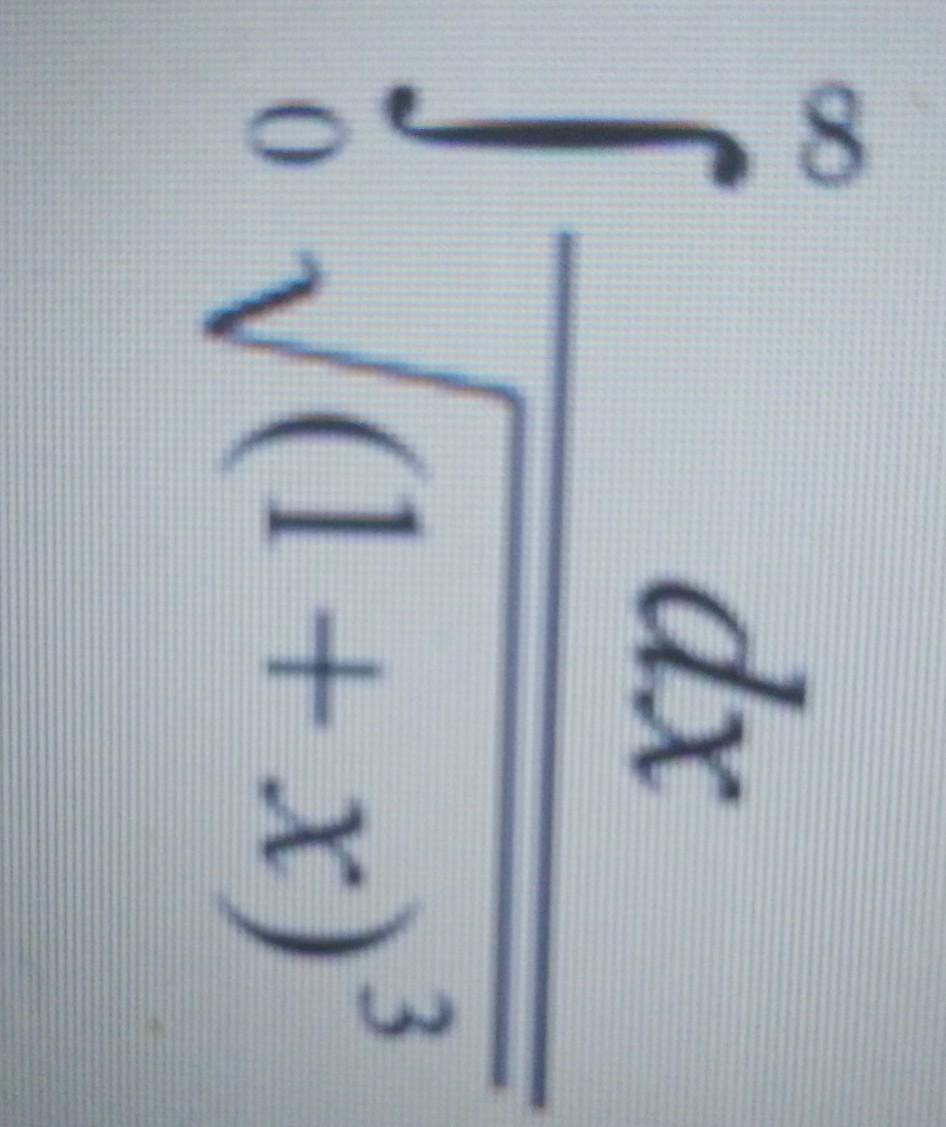Ответы
Ответ дал:
1
Поскольку несобственный интеграл сходится, то сходиться будет интеграл
(первый признак сравнения).
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад