Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
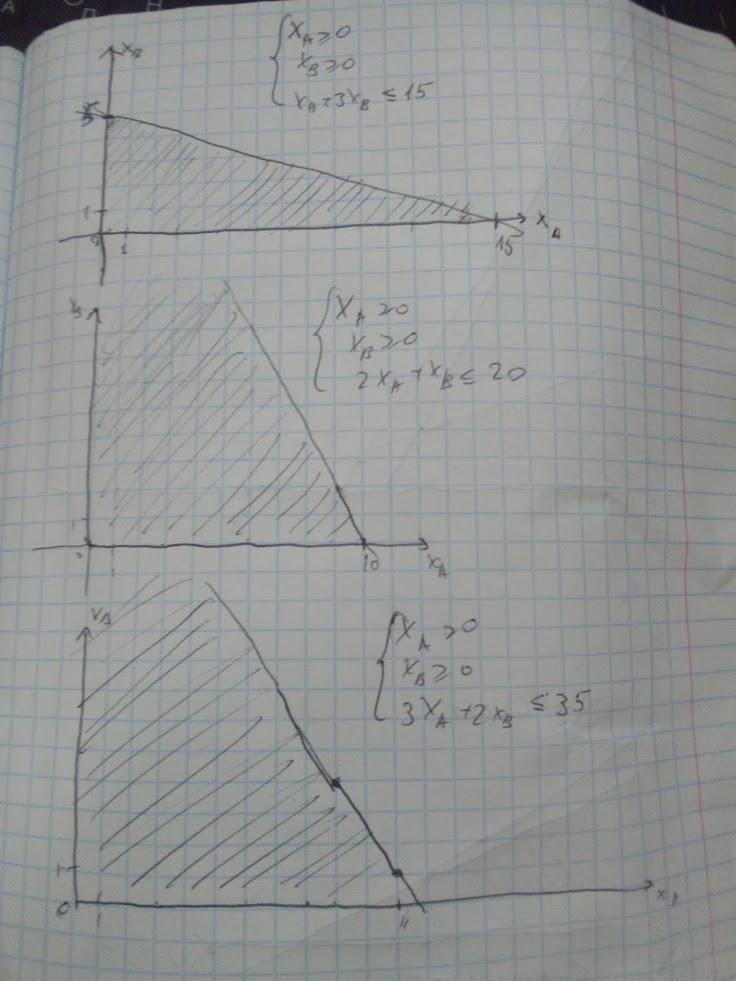
Для начала построим ограничения (картинка 1). Это области под прямыми . На рисунке они построены в первой четверти, то есть
.
Теперь пересечем эти ограничения (график 1 на рисунке 2). Получили область, ограниченную графиками
Рассмотрим всевозможные , то есть прямые, параллельные
. При этом, максимальное
такое, что
еще имеет общие точки с областью ограничений и будет ответом. Как видно из графика 2 на рисунке 2, при таком
прямая проходит через точку пересечения
. Таким образом,
Приложения:

Аноним:
Тут еще вектор-градиент целевой функции, указывает направление максимизации... Не видно по графику где максимум... Если вы подобрали точку - лучше уж все пересечения найти и подставлять их координаты => найти наибольшее значение целевой функции
Да, вектор-градиент {5, 10}. Суть в том, что целевая функция возрастает "внутрь" первой четверти. При этом максимум (если и достигается), то достигается на границе. Ограничения нам дают компактное множество, так что решение есть. Прямые 5xa+10xb=const не параллельны прямым из ограничения, так что пересекать будет в точке.
Далее выбор не большой - подходят только точки из пересечения прямых в ограничении. Да, неплохо бы было найти все пересечения и подставить в целевую функцию, но из графика достаточно видно, что это должна быть точка (9;10)
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
