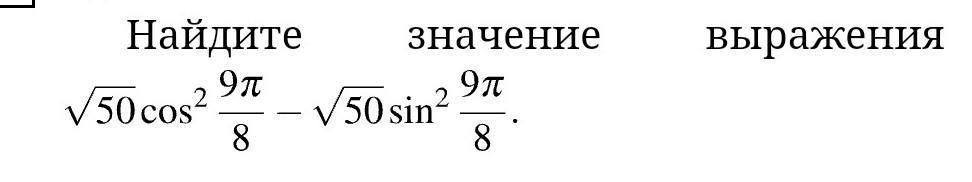Ответы
Ответ дал:
7
√50cos² 9π/8 - √50sin² 9π/8=√50(cos²9π/8-sin²9π/8)=
=√50cos(2*9π/8)=√50cos9π/4=√50cos(8π/4+π/4)=
=√50cos(2π+π/4)=√50cosπ/4=√50*√2/2=√100/2=10/2=5
Ответ дал:
1
Ответ:
5.
Пошаговое объяснение:
√50cos^2 9π/8 - √50sin^2 9π/8 = √50•(cos^2 9π/8 - sin^2 9π/8) = 5√2•( cos (2•9π/8) ) = 5√2 • cos(9π/4) = 5√2 • cos(2π + π/4) = 5√2 • cos(π/4) = 5√2 • √2/2 = 5•2/2 = 5.
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
8 лет назад