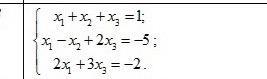Question

Решите по формулам Крамера пожалуйста

Answer 1

Находим определитель матрицы.

1 1 1

1 -1 2

2 0 3

 = 1·(-1)·3 + 1·2·2 + 1·1·0 - 1·(-1)·2 - 1·2·0 - 1·1·3 = -3 + 4 + 0 + 2 - 0 - 3 = 0.

Если определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, то есть несовместна.

Так как по формулам Крамера х1 = Δ1/Δ, то данную системе нельзя решить - деление на ноль.