Ответы
Ответ дал:
2
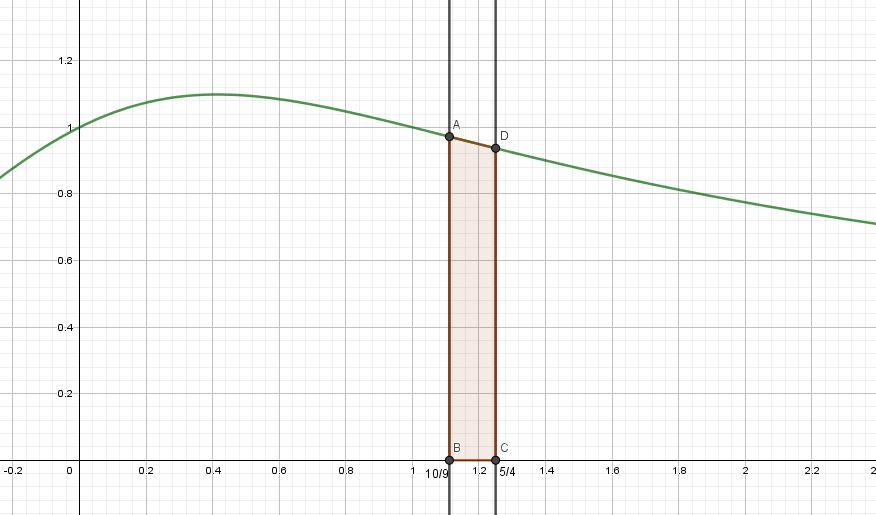
Стандартными способами решить интеграл никак, но графически можно найти площадь фигуры, ограниченными линиями x = 5/4 и x = 10/9. Из школьного курса мы делали полное исследование функции. Не составит труда Вам это вспомнить и построить график.
Найдем точки пересечения графика функции с прямыми x = 5/4 и x = 10/9
Вот и на рисунку есть примерный график. Похож на прямоугольную трапецию и не трудно найти ее площадь. Высота трапеции:
Приложения:
Simba2017:
мне кажется все же не тот метод должен быть....хотя мне ваш метод нравится)
Ну интеграл бесполезно считать :) https://prnt.sc/pieu2w
верю)
а его первообразная какая будет?) или не получается найти?
мы просто по этому методу не решали никогда
а площадь фигуры, ограниченными линиями? это школьный курс
я с алгеброй не дружу :D
теперь нужно попытаться понять что как)) Спасибо Вам!
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад