Question

вычислите площадь фигуры ограниченной линиями у=х^2, у=0, х= -2, х=-1

Answer 1

Пошаговое объяснение:

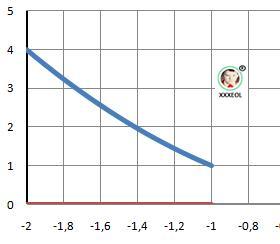
ДАНО: y = x², a = -2, b = -1

РЕШЕНИЕ

$S=\int\limits^b_a {x^2} \, dx=\frac{x^3}{3}$

Вычисляем в переделах интегрирования.

S(-1) = 1/3

S(-2) = 2 2/3

S = 2 2/3 - 1/3 = 2 1/3 - площадь - ответ.

Рисунок к задаче в приложении.